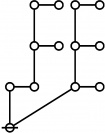
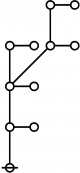
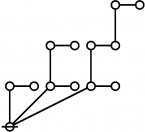
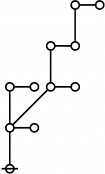
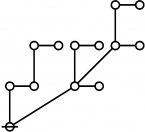
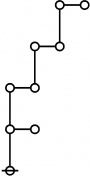
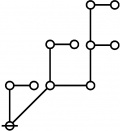
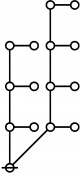
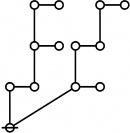
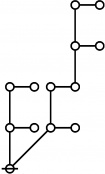
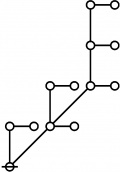
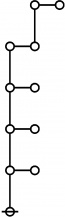
Difference between revisions of "Directory:Jon Awbrey/Papers/Riffs and Rotes"
Jon Awbrey (talk | contribs) (Idea …) |
Jon Awbrey (talk | contribs) (→Idea) |
||
| Line 3: | Line 3: | ||
==Idea== | ==Idea== | ||
| + | |||
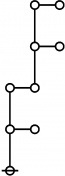
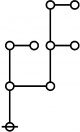
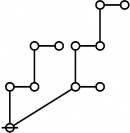
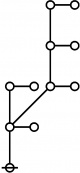
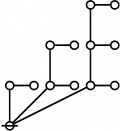
| + | Let <math>\text{p}_i\!</math> be the <math>i^\text{th}\!</math> prime, taking <math>2\!</math> as <math>1^\text{st}\!</math> prime in the sequence that begins as follows: | ||
| + | |||
| + | : <math>\text{p}_1 = 2, \text{p}_2 = 3, \text{p}_3 = 5, \text{p}_4 = 7, \text{p}_5 = 11\!</math> and so on. | ||
{| align="center" cellpadding="20" width="100%" | {| align="center" cellpadding="20" width="100%" | ||
Revision as of 03:02, 3 February 2010
Idea
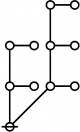
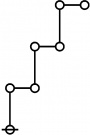
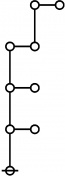
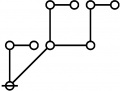
Let \(\text{p}_i\!\) be the \(i^\text{th}\!\) prime, taking \(2\!\) as \(1^\text{st}\!\) prime in the sequence that begins as follows:
\[\text{p}_1 = 2, \text{p}_2 = 3, \text{p}_3 = 5, \text{p}_4 = 7, \text{p}_5 = 11\!\] and so on.
| \(\cdots\) |
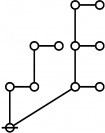
Riffs in Numerical Order
|
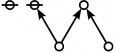
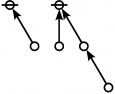
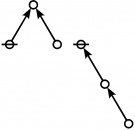
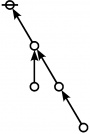
\(1\!\) \(\begin{array}{l} \varnothing \\ 1 \end{array}\) |
\(\text{p}\!\) \(\begin{array}{l} 1\!:\!1 \\ 2 \end{array}\) |
\(\text{p}_\text{p}\!\) \(\begin{array}{l} 2\!:\!1 \\ 3 \end{array}\) |
\(\text{p}^\text{p}\!\) \(\begin{array}{l} 1\!:\!2 \\ 4 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 3\!:\!1 \\ 5 \end{array}\) |
|
\(\text{p} \text{p}_\text{p}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 \\ 6 \end{array}\) |
\(\text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 4\!:\!1 \\ 7 \end{array}\) |
\(\text{p}^{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!3 \\ 8 \end{array}\) |
\(\text{p}_\text{p}^\text{p}\!\) \(\begin{array}{l} 2\!:\!2 \\ 9 \end{array}\) |
\(\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 3\!:\!1 \\ 10 \end{array}\) |
|
\(\text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 5\!:\!1 \\ 11 \end{array}\) |
\(\text{p}^\text{p} \text{p}_\text{p}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 \\ 12 \end{array}\) |
\(\text{p}_{\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 6\!:\!1 \\ 13 \end{array}\) |
\(\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 4\!:\!1 \\ 14 \end{array}\) |
\(\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 3\!:\!1 \\ 15 \end{array}\) |
|
\(\text{p}^{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!4 \\ 16 \end{array}\) |
\(\text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 7\!:\!1 \\ 17 \end{array}\) |
\(\text{p} \text{p}_\text{p}^\text{p}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!2 \\ 18 \end{array}\) |
\(\text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 8\!:\!1 \\ 19 \end{array}\) |
\(\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 3\!:\!1 \\ 20 \end{array}\) |
|
\(\text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 4\!:\!1 \\ 21 \end{array}\) |
\(\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 5\!:\!1 \\ 22 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}^\text{p}}\!\) \(\begin{array}{l} 9\!:\!1 \\ 23 \end{array}\) |
\(\text{p}^{\text{p}_\text{p}} \text{p}_\text{p}\!\) \(\begin{array}{l} 1\!:\!3 ~~ 2\!:\!1 \\ 24 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}}^\text{p}\!\) \(\begin{array}{l} 3\!:\!2 \\ 25 \end{array}\) |
|
\(\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 6\!:\!1 \\ 26 \end{array}\) |
\(\text{p}_\text{p}^{\text{p}_\text{p}}\!\) \(\begin{array}{l} 2\!:\!3 \\ 27 \end{array}\) |
\(\text{p}^\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 4\!:\!1 \\ 28 \end{array}\) |
\(\text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 10\!:\!1 \\ 29 \end{array}\) |
\(\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 30 \end{array}\) |
|
\(\text{p}_{\text{p}_{\text{p}_{\text{p}_\text{p}}}}\!\) \(\begin{array}{l} 11\!:\!1 \\ 31 \end{array}\) |
\(\text{p}^{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!5 \\ 32 \end{array}\) |
\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 5\!:\!1 \\ 33 \end{array}\) |
\(\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 7\!:\!1 \\ 34 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 3\!:\!1 ~~ 4\!:\!1 \\ 35 \end{array}\) |
|
\(\text{p}^\text{p} \text{p}_\text{p}^\text{p}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 2\!:\!2 \\ 36 \end{array}\) |
\(\text{p}_{\text{p}^\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 12\!:\!1 \\ 37 \end{array}\) |
\(\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 8\!:\!1 \\ 38 \end{array}\) |
\(\text{p}_\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 6\!:\!1 \\ 39 \end{array}\) |
\(\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!3 ~~ 3\!:\!1 \\ 40 \end{array}\) |
|
\(\text{p}_{\text{p}_{\text{p} \text{p}_\text{p}}}\!\) \(\begin{array}{l} 13\!:\!1 \\ 41 \end{array}\) |
\(\text{p} \text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 ~~ 4\!:\!1 \\ 42 \end{array}\) |
\(\text{p}_{\text{p} \text{p}_{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 14\!:\!1 \\ 43 \end{array}\) |
\(\text{p}^\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 5\!:\!1 \\ 44 \end{array}\) |
\(\text{p}_\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 2\!:\!2 ~~ 3\!:\!1 \\ 45 \end{array}\) |
|
\(\text{p} \text{p}_{\text{p}_\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 9\!:\!1 \\ 46 \end{array}\) |
\(\text{p}_{\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 15\!:\!1 \\ 47 \end{array}\) |
\(\text{p}^{\text{p}^\text{p}} \text{p}_\text{p}\!\) \(\begin{array}{l} 1\!:\!4 ~~ 2\!:\!1 \\ 48 \end{array}\) |
\(\text{p}_{\text{p}^\text{p}}^\text{p}\!\) \(\begin{array}{l} 4\!:\!2 \\ 49 \end{array}\) |
\(\text{p} \text{p}_{\text{p}_\text{p}}^\text{p}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 3\!:\!2 \\ 50 \end{array}\) |
|
\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 7\!:\!1 \\ 51 \end{array}\) |
\(\text{p}^\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 6\!:\!1 \\ 52 \end{array}\) |
\(\text{p}_{\text{p}^{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 16\!:\!1 \\ 53 \end{array}\) |
\(\text{p} \text{p}_\text{p}^{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!3 \\ 54 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 3\!:\!1 ~~ 5\!:\!1 \\ 55 \end{array}\) |
|
\(\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!3 ~~ 4\!:\!1 \\ 56 \end{array}\) |
\(\text{p}_\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 8\!:\!1 \\ 57 \end{array}\) |
\(\text{p} \text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 10\!:\!1 \\ 58 \end{array}\) |
\(\text{p}_{\text{p}_{\text{p}_{\text{p}^\text{p}}}}\!\) \(\begin{array}{l} 17\!:\!1 \\ 59 \end{array}\) |
\(\text{p}^\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 60 \end{array}\) |
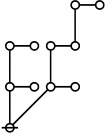
Rotes in Numerical Order
|
\(1\!\) \(\begin{array}{l} \varnothing \\ 1 \end{array}\) |
\(\text{p}\!\) \(\begin{array}{l} 1\!:\!1 \\ 2 \end{array}\) |
\(\text{p}_\text{p}\!\) \(\begin{array}{l} 2\!:\!1 \\ 3 \end{array}\) |
\(\text{p}^\text{p}\!\) \(\begin{array}{l} 1\!:\!2 \\ 4 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 3\!:\!1 \\ 5 \end{array}\) |
|
\(\text{p} \text{p}_\text{p}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 \\ 6 \end{array}\) |
\(\text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 4\!:\!1 \\ 7 \end{array}\) |
\(\text{p}^{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!3 \\ 8 \end{array}\) |
\(\text{p}_\text{p}^\text{p}\!\) \(\begin{array}{l} 2\!:\!2 \\ 9 \end{array}\) |
\(\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 3\!:\!1 \\ 10 \end{array}\) |
|
\(\text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 5\!:\!1 \\ 11 \end{array}\) |
\(\text{p}^\text{p} \text{p}_\text{p}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 \\ 12 \end{array}\) |
\(\text{p}_{\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 6\!:\!1 \\ 13 \end{array}\) |
\(\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 4\!:\!1 \\ 14 \end{array}\) |
\(\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 3\!:\!1 \\ 15 \end{array}\) |
|
\(\text{p}^{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!4 \\ 16 \end{array}\) |
\(\text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 7\!:\!1 \\ 17 \end{array}\) |
\(\text{p} \text{p}_\text{p}^\text{p}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!2 \\ 18 \end{array}\) |
\(\text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 8\!:\!1 \\ 19 \end{array}\) |
\(\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 3\!:\!1 \\ 20 \end{array}\) |
|
\(\text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 4\!:\!1 \\ 21 \end{array}\) |
\(\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 5\!:\!1 \\ 22 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}^\text{p}}\!\) \(\begin{array}{l} 9\!:\!1 \\ 23 \end{array}\) |
\(\text{p}^{\text{p}_\text{p}} \text{p}_\text{p}\!\) \(\begin{array}{l} 1\!:\!3 ~~ 2\!:\!1 \\ 24 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}}^\text{p}\!\) \(\begin{array}{l} 3\!:\!2 \\ 25 \end{array}\) |
|
\(\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 6\!:\!1 \\ 26 \end{array}\) |
\(\text{p}_\text{p}^{\text{p}_\text{p}}\!\) \(\begin{array}{l} 2\!:\!3 \\ 27 \end{array}\) |
\(\text{p}^\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 4\!:\!1 \\ 28 \end{array}\) |
\(\text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 10\!:\!1 \\ 29 \end{array}\) |
\(\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 30 \end{array}\) |
|
\(\text{p}_{\text{p}_{\text{p}_{\text{p}_\text{p}}}}\!\) \(\begin{array}{l} 11\!:\!1 \\ 31 \end{array}\) |
\(\text{p}^{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!5 \\ 32 \end{array}\) |
\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 5\!:\!1 \\ 33 \end{array}\) |
\(\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 7\!:\!1 \\ 34 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 3\!:\!1 ~~ 4\!:\!1 \\ 35 \end{array}\) |
|
\(\text{p}^\text{p} \text{p}_\text{p}^\text{p}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 2\!:\!2 \\ 36 \end{array}\) |
\(\text{p}_{\text{p}^\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 12\!:\!1 \\ 37 \end{array}\) |
\(\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 8\!:\!1 \\ 38 \end{array}\) |
\(\text{p}_\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 6\!:\!1 \\ 39 \end{array}\) |
\(\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!3 ~~ 3\!:\!1 \\ 40 \end{array}\) |
|
\(\text{p}_{\text{p}_{\text{p} \text{p}_\text{p}}}\!\) \(\begin{array}{l} 13\!:\!1 \\ 41 \end{array}\) |
\(\text{p} \text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 ~~ 4\!:\!1 \\ 42 \end{array}\) |
\(\text{p}_{\text{p} \text{p}_{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 14\!:\!1 \\ 43 \end{array}\) |
\(\text{p}^\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 5\!:\!1 \\ 44 \end{array}\) |
\(\text{p}_\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 2\!:\!2 ~~ 3\!:\!1 \\ 45 \end{array}\) |
|
\(\text{p} \text{p}_{\text{p}_\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 9\!:\!1 \\ 46 \end{array}\) |
\(\text{p}_{\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 15\!:\!1 \\ 47 \end{array}\) |
\(\text{p}^{\text{p}^\text{p}} \text{p}_\text{p}\!\) \(\begin{array}{l} 1\!:\!4 ~~ 2\!:\!1 \\ 48 \end{array}\) |
\(\text{p}_{\text{p}^\text{p}}^\text{p}\!\) \(\begin{array}{l} 4\!:\!2 \\ 49 \end{array}\) |
\(\text{p} \text{p}_{\text{p}_\text{p}}^\text{p}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 3\!:\!2 \\ 50 \end{array}\) |
|
\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 7\!:\!1 \\ 51 \end{array}\) |
\(\text{p}^\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 6\!:\!1 \\ 52 \end{array}\) |
\(\text{p}_{\text{p}^{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 16\!:\!1 \\ 53 \end{array}\) |
\(\text{p} \text{p}_\text{p}^{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!3 \\ 54 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 3\!:\!1 ~~ 5\!:\!1 \\ 55 \end{array}\) |
|
\(\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!3 ~~ 4\!:\!1 \\ 56 \end{array}\) |
\(\text{p}_\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 8\!:\!1 \\ 57 \end{array}\) |
\(\text{p} \text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 10\!:\!1 \\ 58 \end{array}\) |
\(\text{p}_{\text{p}_{\text{p}_{\text{p}^\text{p}}}}\!\) \(\begin{array}{l} 17\!:\!1 \\ 59 \end{array}\) |
\(\text{p}^\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 60 \end{array}\) |
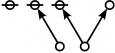
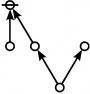
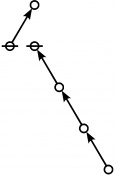
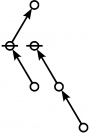
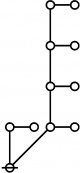
Selected Sequences
A061396
- Number of "rooted index-functional forests" (Riffs) on n nodes.
- Number of "rooted odd trees with only exponent symmetries" (Rotes) on 2n+1 nodes.