Difference between revisions of "Directory:Jon Awbrey/Papers/Riffs and Rotes"
Jon Awbrey (talk | contribs) (Riffs and Rotes in Numerical Order) |
Jon Awbrey (talk | contribs) (update) |
||
| (73 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{DISPLAYTITLE:Riffs and Rotes}} | {{DISPLAYTITLE:Riffs and Rotes}} | ||
| − | __TOC__ | + | <div class="nonumtoc">__TOC__</div> |
| + | |||
| + | ==Idea== | ||
| + | |||
| + | Let <math>\text{p}_i\!</math> be the <math>i^\text{th}\!</math> prime, where the positive integer <math>i\!</math> is called the ''index'' of the prime <math>\text{p}_i\!</math> and the indices are taken in such a way that <math>\text{p}_1 = 2.\!</math> Thus the sequence of primes begins as follows: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \text{p}_1 = 2, & | ||
| + | \text{p}_2 = 3, & | ||
| + | \text{p}_3 = 5, & | ||
| + | \text{p}_4 = 7, & | ||
| + | \text{p}_5 = 11, & | ||
| + | \text{p}_6 = 13, & | ||
| + | \text{p}_7 = 17, & | ||
| + | \text{p}_8 = 19, & | ||
| + | \ldots | ||
| + | \end{matrix}</math> | ||
| + | |} | ||
| + | |||
| + | The prime factorization of a positive integer <math>n\!</math> can be written in the following form: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | <math>n ~=~ \prod_{k = 1}^{\ell} \text{p}_{i(k)}^{j(k)},\!</math> | ||
| + | |} | ||
| + | |||
| + | where <math>\text{p}_{i(k)}^{j(k)}\!</math> is the <math>k^\text{th}\!</math> prime power in the factorization and <math>\ell\!</math> is the number of distinct prime factors dividing <math>n.\!</math> The factorization of <math>1\!</math> is defined as <math>1\!</math> in accord with the convention that an empty product is equal to <math>1.\!</math> | ||
| + | |||
| + | Let <math>I(n)\!</math> be the set of indices of primes that divide <math>n\!</math> and let <math>j(i, n)\!</math> be the number of times that <math>\text{p}_i\!</math> divides <math>n.\!</math> Then the prime factorization of <math>n\!</math> can be written in the following alternative form: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | <math>n ~=~ \prod_{i \in I(n)} \text{p}_{i}^{j(i, n)}.\!</math> | ||
| + | |} | ||
| + | |||
| + | For example: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | 123456789 | ||
| + | & = & 3^2 \cdot 3607 \cdot 3803 | ||
| + | & = & \text{p}_2^2 \text{p}_{504}^1 \text{p}_{529}^1. | ||
| + | \end{matrix}</math> | ||
| + | |} | ||
| + | |||
| + | Each index <math>i\!</math> and exponent <math>j\!</math> appearing in the prime factorization of a positive integer <math>n\!</math> is itself a positive integer, and thus has a prime factorization of its own. | ||
| + | |||
| + | Continuing with the same example, the index <math>504\!</math> has the factorization <math>2^3 \cdot 3^2 \cdot 7 = \text{p}_1^3 \text{p}_2^2 \text{p}_4^1\!</math> and the index <math>529\!</math> has the factorization <math>{23}^2 = \text{p}_9^2.\!</math> Taking this information together with previously known factorizations allows the following replacements to be made in the expression above: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | | ||
| + | <math>\begin{array}{rcl} | ||
| + | 2 & \mapsto & \text{p}_1^1 | ||
| + | \\[6pt] | ||
| + | 504 & \mapsto & \text{p}_1^3 \text{p}_2^2 \text{p}_4^1 | ||
| + | \\[6pt] | ||
| + | 529 & \mapsto & \text{p}_9^2 | ||
| + | \end{array}</math> | ||
| + | |} | ||
| + | |||
| + | This leads to the following development: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | 123456789 | ||
| + | & = & \text{p}_2^2 \text{p}_{504}^1 \text{p}_{529}^1 | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_{\text{p}_1^1}^{\text{p}_1^1} \text{p}_{\text{p}_1^3 \text{p}_2^2 \text{p}_4^1}^1 \text{p}_{\text{p}_9^2}^1 | ||
| + | \end{array}</math> | ||
| + | |} | ||
| + | |||
| + | Continuing to replace every index and exponent with its factorization produces the following development: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | 123456789 | ||
| + | & = & \text{p}_2^2 \text{p}_{504}^1 \text{p}_{529}^1 | ||
| + | \\[18pt] | ||
| + | & = & \text{p}_{\text{p}_1^1}^{\text{p}_1^1} \text{p}_{\text{p}_1^3 \text{p}_2^2 \text{p}_4^1}^1 \text{p}_{\text{p}_9^2}^1 | ||
| + | \\[18pt] | ||
| + | & = & \text{p}_{\text{p}_1^1}^{\text{p}_1^1} \text{p}_{\text{p}_1^{\text{p}_2^1} \text{p}_{\text{p}_1^1}^{\text{p}_1^1} \text{p}_{\text{p}_1^2}^1}^1 \text{p}_{\text{p}_{\text{p}_2^2}^{\text{p}_1^1}}^1 | ||
| + | \\[18pt] | ||
| + | & = & \text{p}_{\text{p}_1^1}^{\text{p}_1^1} \text{p}_{\text{p}_1^{\text{p}_{\text{p}_1^1}^1} \text{p}_{\text{p}_1^1}^{\text{p}_1^1} \text{p}_{\text{p}_1^{\text{p}_1^1}}^1}^1 \text{p}_{\text{p}_{\text{p}_{\text{p}_1^1}^{\text{p}_1^1}}^{\text{p}_1^1}}^1 | ||
| + | \end{array}</math> | ||
| + | |} | ||
| + | |||
| + | The <math>1\!</math>'s that appear as indices and exponents are formally redundant, conveying no information apart from the places they occupy in the resulting syntactic structure. Leaving them tacit produces the following expression: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | 123456789 | ||
| + | & = & \text{p}_{\text{p}}^{\text{p}} \text{p}_{\text{p}^{\text{p}_{\text{p}}} \text{p}_{\text{p}}^{\text{p}} \text{p}_{\text{p}^{\text{p}}}} \text{p}_{\text{p}_{\text{p}_{\text{p}}^{\text{p}}}^{\text{p}}} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| + | |||
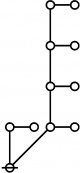
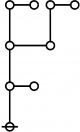
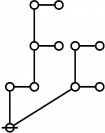
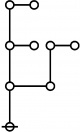
| + | The pattern of indices and exponents illustrated here is called a ''doubly recursive factorization'', or ''DRF''. Applying the same procedure to any positive integer <math>n\!</math> produces an expression called the DRF of <math>n.\!</math> If <math>\mathbb{M}</math> is the set of positive integers, <math>\mathcal{L}</math> is the set of DRF expressions, and the mapping defined by the factorization process is denoted <math>\operatorname{drf} : \mathbb{M} \to \mathcal{L},</math> then the doubly recursive factorization of <math>n\!</math> is denoted <math>\operatorname{drf}(n).\!</math> | ||
| + | |||
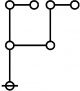
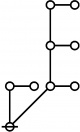
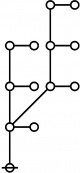
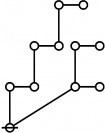
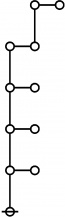
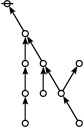
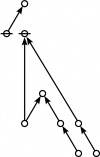
| + | The forms of DRF expressions can be mapped into either one of two classes of graph-theoretical structures, called ''riffs'' and ''rotes'', respectively. | ||
| + | |||
| + | {| align=center cellpadding="6" width="90%" | ||
| + | |- | ||
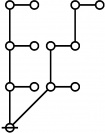
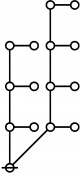
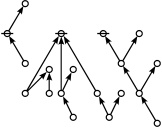
| + | | <math>\operatorname{riff}(123456789)</math> is the following digraph: | ||
| + | |- | ||
| + | | align=center | [[Image:Riff 123456789 Big.jpg|220px]] | ||
| + | |- | ||
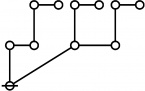
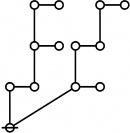
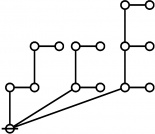
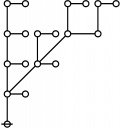
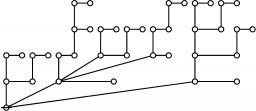
| + | | <math>\operatorname{rote}(123456789)</math> is the following graph: | ||
| + | |- | ||
| + | | align=center | [[Image:Rote 123456789 Big.jpg|345px]] | ||
| + | |} | ||
==Riffs in Numerical Order== | ==Riffs in Numerical Order== | ||
| − | {| align="center" border="1" cellpadding=" | + | {| align="center" border="1" cellpadding="12" |
|+ style="height:25px" | <math>\text{Riffs in Numerical Order}\!</math> | |+ style="height:25px" | <math>\text{Riffs in Numerical Order}\!</math> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p> </p><br> | <p> </p><br> | ||
| − | <p> | + | <p><math>1\!</math></p><br> |
<p><math>\begin{array}{l} \varnothing \\ 1 \end{array}</math></p> | <p><math>\begin{array}{l} \varnothing \\ 1 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
| Line 262: | Line 374: | ||
{| align="center" border="1" cellpadding="6" | {| align="center" border="1" cellpadding="6" | ||
| + | |+ style="height:25px" | <math>\text{Rotes in Numerical Order}\!</math> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 1 Big.jpg|20px]]</p><br> | <p>[[Image:Rote 1 Big.jpg|20px]]</p><br> | ||
| + | <p><math>1\!</math></p><br> | ||
<p><math>\begin{array}{l} \varnothing \\ 1 \end{array}</math></p> | <p><math>\begin{array}{l} \varnothing \\ 1 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 2 Big.jpg|40px]]</p><br> | <p>[[Image:Rote 2 Big.jpg|40px]]</p><br> | ||
| + | <p><math>\text{p}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!1 \\ 2 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!1 \\ 2 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 3 Big.jpg|40px]]</p><br> | <p>[[Image:Rote 3 Big.jpg|40px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p}\!</math></p><br> | ||
<p><math>\begin{array}{l} 2\!:\!1 \\ 3 \end{array}</math></p> | <p><math>\begin{array}{l} 2\!:\!1 \\ 3 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 4 Big.jpg|65px]]</p><br> | <p>[[Image:Rote 4 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!2 \\ 4 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!2 \\ 4 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 5 Big.jpg|40px]]</p><br> | <p>[[Image:Rote 5 Big.jpg|40px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 3\!:\!1 \\ 5 \end{array}</math></p> | <p><math>\begin{array}{l} 3\!:\!1 \\ 5 \end{array}</math></p> | ||
|- | |- | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 6 Big.jpg|80px]]</p><br> | <p>[[Image:Rote 6 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 \\ 6 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 \\ 6 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 7 Big.jpg|65px]]</p><br> | <p>[[Image:Rote 7 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 4\!:\!1 \\ 7 \end{array}</math></p> | <p><math>\begin{array}{l} 4\!:\!1 \\ 7 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 8 Big.jpg|65px]]</p><br> | <p>[[Image:Rote 8 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!3 \\ 8 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!3 \\ 8 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 9 Big.jpg|80px]]</p><br> | <p>[[Image:Rote 9 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p}^\text{p}\!</math></p><br> | ||
<p><math>\begin{array}{l} 2\!:\!2 \\ 9 \end{array}</math></p> | <p><math>\begin{array}{l} 2\!:\!2 \\ 9 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 10 Big.jpg|80px]]</p><br> | <p>[[Image:Rote 10 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!1 ~~ 3\!:\!1 \\ 10 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!1 ~~ 3\!:\!1 \\ 10 \end{array}</math></p> | ||
|- | |- | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 11 Big.jpg|40px]]</p><br> | <p>[[Image:Rote 11 Big.jpg|40px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 5\!:\!1 \\ 11 \end{array}</math></p> | <p><math>\begin{array}{l} 5\!:\!1 \\ 11 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 12 Big.jpg|105px]]</p><br> | <p>[[Image:Rote 12 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_\text{p}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 \\ 12 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 \\ 12 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 13 Big.jpg|80px]]</p><br> | <p>[[Image:Rote 13 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p} \text{p}_\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 6\!:\!1 \\ 13 \end{array}</math></p> | <p><math>\begin{array}{l} 6\!:\!1 \\ 13 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 14 Big.jpg|105px]]</p><br> | <p>[[Image:Rote 14 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!1 ~~ 4\!:\!1 \\ 14 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!1 ~~ 4\!:\!1 \\ 14 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 15 Big.jpg|80px]]</p><br> | <p>[[Image:Rote 15 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 2\!:\!1 ~~ 3\!:\!1 \\ 15 \end{array}</math></p> | <p><math>\begin{array}{l} 2\!:\!1 ~~ 3\!:\!1 \\ 15 \end{array}</math></p> | ||
|- | |- | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 16 Big.jpg|90px]]</p><br> | <p>[[Image:Rote 16 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}^\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!4 \\ 16 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!4 \\ 16 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 17 Big.jpg|65px]]</p><br> | <p>[[Image:Rote 17 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p}^\text{p}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 7\!:\!1 \\ 17 \end{array}</math></p> | <p><math>\begin{array}{l} 7\!:\!1 \\ 17 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 18 Big.jpg|120px]]</p><br> | <p>[[Image:Rote 18 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p}^\text{p}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!1 ~~ 2\!:\!2 \\ 18 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!1 ~~ 2\!:\!2 \\ 18 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 19 Big.jpg|65px]]</p><br> | <p>[[Image:Rote 19 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^{\text{p}_\text{p}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 8\!:\!1 \\ 19 \end{array}</math></p> | <p><math>\begin{array}{l} 8\!:\!1 \\ 19 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 20 Big.jpg|105px]]</p><br> | <p>[[Image:Rote 20 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!2 ~~ 3\!:\!1 \\ 20 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!2 ~~ 3\!:\!1 \\ 20 \end{array}</math></p> | ||
|- | |- | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 21 Big.jpg|105px]]</p><br> | <p>[[Image:Rote 21 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 2\!:\!1 ~~ 4\!:\!1 \\ 21 \end{array}</math></p> | <p><math>\begin{array}{l} 2\!:\!1 ~~ 4\!:\!1 \\ 21 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 22 Big.jpg|80px]]</p><br> | <p>[[Image:Rote 22 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!1 ~~ 5\!:\!1 \\ 22 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!1 ~~ 5\!:\!1 \\ 22 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 23 Big.jpg|80px]]</p><br> | <p>[[Image:Rote 23 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}^\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 9\!:\!1 \\ 23 \end{array}</math></p> | <p><math>\begin{array}{l} 9\!:\!1 \\ 23 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 24 Big.jpg|105px]]</p><br> | <p>[[Image:Rote 24 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_\text{p}} \text{p}_\text{p}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!3 ~~ 2\!:\!1 \\ 24 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!3 ~~ 2\!:\!1 \\ 24 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 25 Big.jpg|80px]]</p><br> | <p>[[Image:Rote 25 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}}^\text{p}\!</math></p><br> | ||
<p><math>\begin{array}{l} 3\!:\!2 \\ 25 \end{array}</math></p> | <p><math>\begin{array}{l} 3\!:\!2 \\ 25 \end{array}</math></p> | ||
|- | |- | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 26 Big.jpg|120px]]</p><br> | <p>[[Image:Rote 26 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!1 ~~ 6\!:\!1 \\ 26 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!1 ~~ 6\!:\!1 \\ 26 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 27 Big.jpg|80px]]</p><br> | <p>[[Image:Rote 27 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p}^{\text{p}_\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 2\!:\!3 \\ 27 \end{array}</math></p> | <p><math>\begin{array}{l} 2\!:\!3 \\ 27 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 28 Big.jpg|130px]]</p><br> | <p>[[Image:Rote 28 Big.jpg|130px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!2 ~~ 4\!:\!1 \\ 28 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!2 ~~ 4\!:\!1 \\ 28 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 29 Big.jpg|80px]]</p><br> | <p>[[Image:Rote 29 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 10\!:\!1 \\ 29 \end{array}</math></p> | <p><math>\begin{array}{l} 10\!:\!1 \\ 29 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 30 Big.jpg|120px]]</p><br> | <p>[[Image:Rote 30 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 30 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 30 \end{array}</math></p> | ||
|- | |- | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 31 Big.jpg|40px]]</p><br> | <p>[[Image:Rote 31 Big.jpg|40px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p}_{\text{p}_\text{p}}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 11\!:\!1 \\ 31 \end{array}</math></p> | <p><math>\begin{array}{l} 11\!:\!1 \\ 31 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 32 Big.jpg|65px]]</p><br> | <p>[[Image:Rote 32 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!5 \\ 32 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!5 \\ 32 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 33 Big.jpg|80px]]</p><br> | <p>[[Image:Rote 33 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 2\!:\!1 ~~ 5\!:\!1 \\ 33 \end{array}</math></p> | <p><math>\begin{array}{l} 2\!:\!1 ~~ 5\!:\!1 \\ 33 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 34 Big.jpg|105px]]</p><br> | <p>[[Image:Rote 34 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!1 ~~ 7\!:\!1 \\ 34 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!1 ~~ 7\!:\!1 \\ 34 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 35 Big.jpg|105px]]</p><br> | <p>[[Image:Rote 35 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 3\!:\!1 ~~ 4\!:\!1 \\ 35 \end{array}</math></p> | <p><math>\begin{array}{l} 3\!:\!1 ~~ 4\!:\!1 \\ 35 \end{array}</math></p> | ||
|- | |- | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 36 Big.jpg|145px]]</p><br> | <p>[[Image:Rote 36 Big.jpg|145px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_\text{p}^\text{p}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!2 ~~ 2\!:\!2 \\ 36 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!2 ~~ 2\!:\!2 \\ 36 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 37 Big.jpg|105px]]</p><br> | <p>[[Image:Rote 37 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^\text{p} \text{p}_\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 12\!:\!1 \\ 37 \end{array}</math></p> | <p><math>\begin{array}{l} 12\!:\!1 \\ 37 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 38 Big.jpg|105px]]</p><br> | <p>[[Image:Rote 38 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!1 ~~ 8\!:\!1 \\ 38 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!1 ~~ 8\!:\!1 \\ 38 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 39 Big.jpg|120px]]</p><br> | <p>[[Image:Rote 39 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 2\!:\!1 ~~ 6\!:\!1 \\ 39 \end{array}</math></p> | <p><math>\begin{array}{l} 2\!:\!1 ~~ 6\!:\!1 \\ 39 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 40 Big.jpg|105px]]</p><br> | <p>[[Image:Rote 40 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!3 ~~ 3\!:\!1 \\ 40 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!3 ~~ 3\!:\!1 \\ 40 \end{array}</math></p> | ||
|- | |- | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 41 Big.jpg|80px]]</p><br> | <p>[[Image:Rote 41 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p} \text{p}_\text{p}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 13\!:\!1 \\ 41 \end{array}</math></p> | <p><math>\begin{array}{l} 13\!:\!1 \\ 41 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 42 Big.jpg|145px]]</p><br> | <p>[[Image:Rote 42 Big.jpg|145px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 ~~ 4\!:\!1 \\ 42 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 ~~ 4\!:\!1 \\ 42 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 43 Big.jpg|105px]]</p><br> | <p>[[Image:Rote 43 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p} \text{p}_{\text{p}^\text{p}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 14\!:\!1 \\ 43 \end{array}</math></p> | <p><math>\begin{array}{l} 14\!:\!1 \\ 43 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 44 Big.jpg|105px]]</p><br> | <p>[[Image:Rote 44 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!2 ~~ 5\!:\!1 \\ 44 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!2 ~~ 5\!:\!1 \\ 44 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 45 Big.jpg|120px]]</p><br> | <p>[[Image:Rote 45 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 2\!:\!2 ~~ 3\!:\!1 \\ 45 \end{array}</math></p> | <p><math>\begin{array}{l} 2\!:\!2 ~~ 3\!:\!1 \\ 45 \end{array}</math></p> | ||
|- | |- | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 46 Big.jpg|120px]]</p><br> | <p>[[Image:Rote 46 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_\text{p}^\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!1 ~~ 9\!:\!1 \\ 46 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!1 ~~ 9\!:\!1 \\ 46 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 47 Big.jpg|80px]]</p><br> | <p>[[Image:Rote 47 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 15\!:\!1 \\ 47 \end{array}</math></p> | <p><math>\begin{array}{l} 15\!:\!1 \\ 47 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 48 Big.jpg|105px]]</p><br> | <p>[[Image:Rote 48 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}^\text{p}} \text{p}_\text{p}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!4 ~~ 2\!:\!1 \\ 48 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!4 ~~ 2\!:\!1 \\ 48 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 49 Big.jpg|80px]]</p><br> | <p>[[Image:Rote 49 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^\text{p}}^\text{p}\!</math></p><br> | ||
<p><math>\begin{array}{l} 4\!:\!2 \\ 49 \end{array}</math></p> | <p><math>\begin{array}{l} 4\!:\!2 \\ 49 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 50 Big.jpg|120px]]</p><br> | <p>[[Image:Rote 50 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_\text{p}}^\text{p}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!1 ~~ 3\!:\!2 \\ 50 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!1 ~~ 3\!:\!2 \\ 50 \end{array}</math></p> | ||
|- | |- | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 51 Big.jpg|105px]]</p><br> | <p>[[Image:Rote 51 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 2\!:\!1 ~~ 7\!:\!1 \\ 51 \end{array}</math></p> | <p><math>\begin{array}{l} 2\!:\!1 ~~ 7\!:\!1 \\ 51 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 52 Big.jpg|145px]]</p><br> | <p>[[Image:Rote 52 Big.jpg|145px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!2 ~~ 6\!:\!1 \\ 52 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!2 ~~ 6\!:\!1 \\ 52 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 53 Big.jpg|90px]]</p><br> | <p>[[Image:Rote 53 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^{\text{p}^\text{p}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 16\!:\!1 \\ 53 \end{array}</math></p> | <p><math>\begin{array}{l} 16\!:\!1 \\ 53 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 54 Big.jpg|120px]]</p><br> | <p>[[Image:Rote 54 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p}^{\text{p}_\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!1 ~~ 2\!:\!3 \\ 54 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!1 ~~ 2\!:\!3 \\ 54 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 55 Big.jpg|80px]]</p><br> | <p>[[Image:Rote 55 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 3\!:\!1 ~~ 5\!:\!1 \\ 55 \end{array}</math></p> | <p><math>\begin{array}{l} 3\!:\!1 ~~ 5\!:\!1 \\ 55 \end{array}</math></p> | ||
|- | |- | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 56 Big.jpg|130px]]</p><br> | <p>[[Image:Rote 56 Big.jpg|130px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!3 ~~ 4\!:\!1 \\ 56 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!3 ~~ 4\!:\!1 \\ 56 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 57 Big.jpg|105px]]</p><br> | <p>[[Image:Rote 57 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 2\!:\!1 ~~ 8\!:\!1 \\ 57 \end{array}</math></p> | <p><math>\begin{array}{l} 2\!:\!1 ~~ 8\!:\!1 \\ 57 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 58 Big.jpg|120px]]</p><br> | <p>[[Image:Rote 58 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!1 ~~ 10\!:\!1 \\ 58 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!1 ~~ 10\!:\!1 \\ 58 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 59 Big.jpg|65px]]</p><br> | <p>[[Image:Rote 59 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p}_{\text{p}^\text{p}}}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 17\!:\!1 \\ 59 \end{array}</math></p> | <p><math>\begin{array}{l} 17\!:\!1 \\ 59 \end{array}</math></p> | ||
| valign="bottom" | | | valign="bottom" | | ||
<p>[[Image:Rote 60 Big.jpg|155px]]</p><br> | <p>[[Image:Rote 60 Big.jpg|155px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
<p><math>\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 60 \end{array}</math></p> | <p><math>\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 60 \end{array}</math></p> | ||
| + | |} | ||
| + | |||
| + | ==Prime Animations== | ||
| + | |||
| + | ===Riffs 1 to 60=== | ||
| + | |||
| + | {| align="center" | ||
| + | | [[Image:Animation Riff 60 x 0.16.gif]] | ||
| + | |} | ||
| + | |||
| + | ===Rotes 1 to 60=== | ||
| + | |||
| + | {| align="center" | ||
| + | | [[Image:Animation Rote 60 x 0.16.gif]] | ||
| + | |} | ||
| + | |||
| + | ==Selected Sequences== | ||
| + | |||
| + | ===A061396=== | ||
| + | |||
| + | * '''Number of "rooted index-functional forests" (Riffs) on n nodes.''' | ||
| + | |||
| + | * '''Number of "rooted odd trees with only exponent symmetries" (Rotes) on 2n+1 nodes.''' | ||
| + | |||
| + | * [http://oeis.org/A061396 OEIS Entry for A061396]. | ||
| + | |||
| + | {| align="center" border="1" width="96%" | ||
| + | |+ style="height:24px" | <math>\text{Prime Factorizations, Riffs, Rotes, and Traversals}\!</math> | ||
| + | |- style="height:50px; background:#f0f0ff" | ||
| + | | | ||
| + | {| cellpadding="12" style="background:#f0f0ff; text-align:center; width:100%" | ||
| + | | width="10%" | <math>\text{Integer}\!</math> | ||
| + | | width="19%" | <math>\text{Factorization}\!</math> | ||
| + | | width="14%" | <math>\text{Notation}\!</math> | ||
| + | | width="19%" | <math>\text{Riff Digraph}\!</math> | ||
| + | | width="19%" | <math>\text{Rote Graph}\!</math> | ||
| + | | width="19%" | <math>\text{Traversal}\!</math> | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| cellpadding="12" style="text-align:center; width:100%" | ||
| + | | width="10%" | <math>1\!</math> | ||
| + | | width="19%" | <math>1\!</math> | ||
| + | | width="14%" | | ||
| + | | width="19%" | | ||
| + | | width="19%" | [[Image:Rote 1 Big.jpg|20px]] | ||
| + | | width="19%" | | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| cellpadding="12" style="text-align:center; width:100%" | ||
| + | | width="10%" | <math>2\!</math> | ||
| + | | width="19%" | <math>\text{p}_1^1\!</math> | ||
| + | | width="14%" | <math>\text{p}\!</math> | ||
| + | | width="19%" | [[Image:Riff 2 Big.jpg|20px]] | ||
| + | | width="19%" | [[Image:Rote 2 Big.jpg|40px]] | ||
| + | | width="19%" | <math>((~))</math> | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| cellpadding="12" style="text-align:center; width:100%" | ||
| + | | width="10%" | <math>3\!</math> | ||
| + | | width="19%" | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_2^1 & = & \text{p}_{\text{p}_1^1}^1 | ||
| + | \end{array}</math> | ||
| + | | width="14%" | <math>\text{p}_\text{p}\!</math> | ||
| + | | width="19%" | [[Image:Riff 3 Big.jpg|40px]] | ||
| + | | width="19%" | [[Image:Rote 3 Big.jpg|40px]] | ||
| + | | width="19%" | <math>(((~))(~))</math> | ||
| + | |- | ||
| + | | <math>4\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_1^2 & = & \text{p}_1^{\text{p}_1^1} | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}^\text{p}\!</math> | ||
| + | | [[Image:Riff 4 Big.jpg|40px]] | ||
| + | | [[Image:Rote 4 Big.jpg|65px]] | ||
| + | | <math>((((~))))</math> | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| cellpadding="12" style="text-align:center; width:100%" | ||
| + | | width="10%" | <math>5\!</math> | ||
| + | | width="19%" | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_3^1 | ||
| + | & = & \text{p}_{\text{p}_2^1}^1 | ||
| + | \\[10pt] | ||
| + | & = & \text{p}_{\text{p}_{\text{p}_1^1}^1}^1 | ||
| + | \end{array}</math> | ||
| + | | width="14%" | <math>\text{p}_{\text{p}_{\text{p}}}\!</math> | ||
| + | | width="19%" | [[Image:Riff 5 Big.jpg|65px]] | ||
| + | | width="19%" | [[Image:Rote 5 Big.jpg|40px]] | ||
| + | | width="19%" | <math>((((~))(~))(~))</math> | ||
| + | |- | ||
| + | | <math>6\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_1^1 \text{p}_2^1 | ||
| + | & = & \text{p}_1^1 \text{p}_{\text{p}_1^1}^1 | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p} \text{p}_{\text{p}}\!</math> | ||
| + | | [[Image:Riff 6 Big.jpg|65px]] | ||
| + | | [[Image:Rote 6 Big.jpg|80px]] | ||
| + | | <math>((~))(((~))(~))</math> | ||
| + | |- | ||
| + | | <math>7\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_4^1 | ||
| + | & = & \text{p}_{\text{p}_1^2}^1 | ||
| + | \\[10pt] | ||
| + | & = & \text{p}_{\text{p}_1^{\text{p}_1^1}}^1 | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}_{\text{p}^{\text{p}}}\!</math> | ||
| + | | [[Image:Riff 7 Big.jpg|65px]] | ||
| + | | [[Image:Rote 7 Big.jpg|65px]] | ||
| + | | <math>(((((~))))(~))</math> | ||
| + | |- | ||
| + | | <math>8\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_1^3 | ||
| + | & = & \text{p}_1^{\text{p}_2^1} | ||
| + | \\[10pt] | ||
| + | & = & \text{p}_1^{\text{p}_{\text{p}_1^1}^1} | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}^{\text{p}_{\text{p}}}\!</math> | ||
| + | | [[Image:Riff 8 Big.jpg|65px]] | ||
| + | | [[Image:Rote 8 Big.jpg|65px]] | ||
| + | | <math>(((((~))(~))))</math> | ||
| + | |- | ||
| + | | <math>9\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_2^2 | ||
| + | & = & \text{p}_{\text{p}_1^1}^{\text{p}_1^1} | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}_\text{p}^\text{p}\!</math> | ||
| + | | [[Image:Riff 9 Big.jpg|40px]] | ||
| + | | [[Image:Rote 9 Big.jpg|80px]] | ||
| + | | <math>(((~))(((~))))</math> | ||
| + | |- | ||
| + | | <math>16\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_1^4 | ||
| + | & = & \text{p}_1^{\text{p}_1^2} | ||
| + | \\[10pt] | ||
| + | & = & \text{p}_1^{\text{p}_1^{\text{p}_1^1}} | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}^{\text{p}^{\text{p}}}\!</math> | ||
| + | | [[Image:Riff 16 Big.jpg|65px]] | ||
| + | | [[Image:Rote 16 Big.jpg|90px]] | ||
| + | | <math>((((((~))))))</math> | ||
| + | |} | ||
| + | |} | ||
| + | |||
| + | ===A062504=== | ||
| + | |||
| + | * '''Triangle in which k-th row lists natural number values for the collection of riffs with k nodes.''' | ||
| + | |||
| + | * [http://oeis.org/A062504 OEIS Entry for A062504]. | ||
| + | |||
| + | {| align="center" | ||
| + | | | ||
| + | <math>\begin{array}{l|l|r} | ||
| + | k | ||
| + | & P_k | ||
| + | = \{ n : \operatorname{riff}(n) ~\text{has}~ k ~\text{nodes} \} | ||
| + | = \{ n : \operatorname{rote}(n) ~\text{has}~ 2k + 1 ~\text{nodes} \} | ||
| + | & |P_k| | ||
| + | \\[10pt] | ||
| + | 0 & \{ 1 \} & 1 | ||
| + | \\ | ||
| + | 1 & \{ 2 \} & 1 | ||
| + | \\ | ||
| + | 2 & \{ 3, 4 \} & 2 | ||
| + | \\ | ||
| + | 3 & \{ 5, 6, 7, 8, 9, 16 \} & 6 | ||
| + | \\ | ||
| + | 4 & \{ 10, 11, 12, 13, 14, 17, 18, 19, 23, 25, 27, 32, 49, 53, 64, 81, 128, 256, 512, 65536 \} & 20 | ||
| + | \end{array}</math> | ||
| + | |} | ||
| + | |||
| + | {| align="center" border="1" width="90%" | ||
| + | |+ style="height:25px" | <math>\text{Prime Factorizations, Riffs, and Rotes}\!</math> | ||
| + | |- style="height:50px; background:#f0f0ff" | ||
| + | | | ||
| + | {| cellpadding="12" style="background:#f0f0ff; text-align:center; width:100%" | ||
| + | | width="10%" | <math>\text{Integer}\!</math> | ||
| + | | width="25%" | <math>\text{Factorization}\!</math> | ||
| + | | width="15%" | <math>\text{Notation}\!</math> | ||
| + | | width="25%" | <math>\text{Riff Digraph}\!</math> | ||
| + | | width="25%" | <math>\text{Rote Graph}\!</math> | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| cellpadding="12" style="text-align:center; width:100%" | ||
| + | | width="10%" | <math>1\!</math> | ||
| + | | width="25%" | <math>1\!</math> | ||
| + | | width="15%" | | ||
| + | | width="25%" | | ||
| + | | width="25%" | [[Image:Rote 1 Big.jpg|20px]] | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| cellpadding="12" style="text-align:center; width:100%" | ||
| + | | width="10%" | <math>2\!</math> | ||
| + | | width="25%" | <math>\text{p}_1^1\!</math> | ||
| + | | width="15%" | <math>\text{p}\!</math> | ||
| + | | width="25%" | [[Image:Riff 2 Big.jpg|20px]] | ||
| + | | width="25%" | [[Image:Rote 2 Big.jpg|40px]] | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| cellpadding="12" style="text-align:center; width:100%" | ||
| + | | width="10%" | <math>3\!</math> | ||
| + | | width="25%" | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_2^1 & = & \text{p}_{\text{p}_1^1}^1 | ||
| + | \end{array}</math> | ||
| + | | width="15%" | <math>\text{p}_\text{p}\!</math> | ||
| + | | width="25%" | [[Image:Riff 3 Big.jpg|40px]] | ||
| + | | width="25%" | [[Image:Rote 3 Big.jpg|40px]] | ||
| + | |- | ||
| + | | <math>4\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_1^2 & = & \text{p}_1^{\text{p}_1^1} | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}^\text{p}\!</math> | ||
| + | | [[Image:Riff 4 Big.jpg|40px]] | ||
| + | | [[Image:Rote 4 Big.jpg|65px]] | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| cellpadding="12" style="text-align:center; width:100%" | ||
| + | | width="10%" | <math>5\!</math> | ||
| + | | width="25%" | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_3^1 | ||
| + | & = & \text{p}_{\text{p}_2^1}^1 | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_{\text{p}_{\text{p}_1^1}^1}^1 | ||
| + | \end{array}</math> | ||
| + | | width="15%" | <math>\text{p}_{\text{p}_{\text{p}}}\!</math> | ||
| + | | width="25%" | [[Image:Riff 5 Big.jpg|65px]] | ||
| + | | width="25%" | [[Image:Rote 5 Big.jpg|40px]] | ||
| + | |- | ||
| + | | <math>6\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_1^1 \text{p}_2^1 | ||
| + | & = & \text{p}_1^1 \text{p}_{\text{p}_1^1}^1 | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p} \text{p}_{\text{p}}\!</math> | ||
| + | | [[Image:Riff 6 Big.jpg|65px]] | ||
| + | | [[Image:Rote 6 Big.jpg|80px]] | ||
| + | |- | ||
| + | | <math>7\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_4^1 | ||
| + | & = & \text{p}_{\text{p}_1^2}^1 | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_{\text{p}_1^{\text{p}_1^1}}^1 | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}_{\text{p}^{\text{p}}}\!</math> | ||
| + | | [[Image:Riff 7 Big.jpg|65px]] | ||
| + | | [[Image:Rote 7 Big.jpg|65px]] | ||
| + | |- | ||
| + | | <math>8\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_1^3 | ||
| + | & = & \text{p}_1^{\text{p}_2^1} | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_1^{\text{p}_{\text{p}_1^1}^1} | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}^{\text{p}_{\text{p}}}\!</math> | ||
| + | | [[Image:Riff 8 Big.jpg|65px]] | ||
| + | | [[Image:Rote 8 Big.jpg|65px]] | ||
| + | |- | ||
| + | | <math>9\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_2^2 | ||
| + | & = & \text{p}_{\text{p}_1^1}^{\text{p}_1^1} | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}_\text{p}^\text{p}\!</math> | ||
| + | | [[Image:Riff 9 Big.jpg|40px]] | ||
| + | | [[Image:Rote 9 Big.jpg|80px]] | ||
| + | |- | ||
| + | | <math>16\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_1^4 | ||
| + | & = & \text{p}_1^{\text{p}_1^2} | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_1^{\text{p}_1^{\text{p}_1^1}} | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}^{\text{p}^{\text{p}}}\!</math> | ||
| + | | [[Image:Riff 16 Big.jpg|65px]] | ||
| + | | [[Image:Rote 16 Big.jpg|90px]] | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| cellpadding="12" style="text-align:center; width:100%" | ||
| + | | width="10%" | <math>10\!</math> | ||
| + | | width="25%" | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_1^1 \text{p}_3^1 | ||
| + | & = & \text{p}_1^1 \text{p}_{\text{p}_2^1}^1 | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_1^1 \text{p}_{\text{p}_{\text{p}_1^1}^1}^1 | ||
| + | \end{array}</math> | ||
| + | | width="15%" | <math>\text{p} \text{p}_{\text{p}_{\text{p}}}\!</math> | ||
| + | | width="25%" | [[Image:Riff 10 Big.jpg|90px]] | ||
| + | | width="25%" | [[Image:Rote 10 Big.jpg|80px]] | ||
| + | |- | ||
| + | | <math>11\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_5^1 | ||
| + | & = & \text{p}_{\text{p}_3^1}^1 | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_{\text{p}_{\text{p}_2^1}^1}^1 | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_{\text{p}_{\text{p}_{\text{p}_1^1}^1}^1}^1 | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math> | ||
| + | | [[Image:Riff 11 Big.jpg|90px]] | ||
| + | | [[Image:Rote 11 Big.jpg|40px]] | ||
| + | |- | ||
| + | | <math>12\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_1^2 \text{p}_2^1 | ||
| + | & = & \text{p}_1^{\text{p}_1^1} \text{p}_{\text{p}_1^1}^1 | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}^{\text{p}} \text{p}_{\text{p}}\!</math> | ||
| + | | [[Image:Riff 12 Big.jpg|65px]] | ||
| + | | [[Image:Rote 12 Big.jpg|105px]] | ||
| + | |- | ||
| + | | <math>13\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_6^1 | ||
| + | & = & \text{p}_{\text{p}_1^1 \text{p}_2^1}^1 | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_{\text{p}_1^1 \text{p}_{\text{p}_1^1}^1}^1 | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}_{\text{p} \text{p}_{\text{p}}}\!</math> | ||
| + | | [[Image:Riff 13 Big.jpg|65px]] | ||
| + | | [[Image:Rote 13 Big.jpg|80px]] | ||
| + | |- | ||
| + | | <math>14\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_1^1 \text{p}_4^1 | ||
| + | & = & \text{p}_1^1 \text{p}_{\text{p}_1^2}^1 | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_1^1 \text{p}_{\text{p}_1^{\text{p}_1^1}}^1 | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p} \text{p}_{\text{p}^{\text{p}}}\!</math> | ||
| + | | [[Image:Riff 14 Big.jpg|90px]] | ||
| + | | [[Image:Rote 14 Big.jpg|105px]] | ||
| + | |- | ||
| + | | <math>17\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_7^1 | ||
| + | & = & \text{p}_{\text{p}_4^1}^1 | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_{\text{p}_{\text{p}_1^2}^1}^1 | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_{\text{p}_{\text{p}_1^{\text{p}_1^1}}^1}^1 | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}_{\text{p}_{\text{p}^{\text{p}}}}\!</math> | ||
| + | | [[Image:Riff 17 Big.jpg|90px]] | ||
| + | | [[Image:Rote 17 Big.jpg|65px]] | ||
| + | |- | ||
| + | | <math>18\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_1^1 \text{p}_2^2 | ||
| + | & = & \text{p}_1^1 \text{p}_{\text{p}_1^1}^{\text{p}_1^1} | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p} \text{p}_{\text{p}}^{\text{p}}\!</math> | ||
| + | | [[Image:Riff 18 Big.jpg|65px]] | ||
| + | | [[Image:Rote 18 Big.jpg|120px]] | ||
| + | |- | ||
| + | | <math>19\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_8^1 | ||
| + | & = & \text{p}_{\text{p}_1^3}^1 | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_{\text{p}_1^{\text{p}_2^1}}^1 | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_{\text{p}_1^{\text{p}_{\text{p}_1^1}^1}}^1 | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}_{\text{p}^{\text{p}_{\text{p}}}}\!</math> | ||
| + | | [[Image:Riff 19 Big.jpg|90px]] | ||
| + | | [[Image:Rote 19 Big.jpg|65px]] | ||
| + | |- | ||
| + | | <math>23\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_9^1 | ||
| + | & = & \text{p}_{\text{p}_2^2}^1 | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_{\text{p}_{\text{p}_1^1}^{\text{p}_1^1}}^1 | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}_{\text{p}_{\text{p}}^{\text{p}}}\!</math> | ||
| + | | [[Image:Riff 23 Big.jpg|65px]] | ||
| + | | [[Image:Rote 23 Big.jpg|80px]] | ||
| + | |- | ||
| + | | <math>25\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_3^2 | ||
| + | & = & \text{p}_{\text{p}_2^1}^{\text{p}_1^1} | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_{\text{p}_{\text{p}_1^1}^1}^{\text{p}_1^1} | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}_{\text{p}_{\text{p}}}^{\text{p}}\!</math> | ||
| + | | [[Image:Riff 25 Big.jpg|65px]] | ||
| + | | [[Image:Rote 25 Big.jpg|80px]] | ||
| + | |- | ||
| + | | <math>27\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_2^3 | ||
| + | & = & \text{p}_{\text{p}_1^1}^{\text{p}_2^1} | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_{\text{p}_1^1}^{\text{p}_{\text{p}_1^1}^1} | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}_{\text{p}}^{\text{p}_{\text{p}}}\!</math> | ||
| + | | [[Image:Riff 27 Big.jpg|65px]] | ||
| + | | [[Image:Rote 27 Big.jpg|80px]] | ||
| + | |- | ||
| + | | <math>32\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_1^5 | ||
| + | & = & \text{p}_1^{\text{p}_3^1} | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_1^{\text{p}_{\text{p}_2^1}^1} | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_1^{\text{p}_{\text{p}_{\text{p}_1^1}^1}^1} | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}^{\text{p}_{\text{p}_{\text{p}}}}\!</math> | ||
| + | | [[Image:Riff 32 Big.jpg|90px]] | ||
| + | | [[Image:Rote 32 Big.jpg|65px]] | ||
| + | |- | ||
| + | | <math>49\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_4^2 | ||
| + | & = & \text{p}_{\text{p}_1^2}^{\text{p}_1^1} | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_{\text{p}_1^{\text{p}_1^1}}^{\text{p}_1^1} | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}_{\text{p}^{\text{p}}}^{\text{p}}\!</math> | ||
| + | | [[Image:Riff 49 Big.jpg|65px]] | ||
| + | | [[Image:Rote 49 Big.jpg|80px]] | ||
| + | |- | ||
| + | | <math>53\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_{16}^1 | ||
| + | & = & \text{p}_{\text{p}_1^4}^1 | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_{\text{p}_1^{\text{p}_1^2}}^1 | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_{\text{p}_1^{\text{p}_1^{\text{p}_1^1}}}^1 | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}_{\text{p}^{\text{p}^{\text{p}}}}\!</math> | ||
| + | | [[Image:Riff 53 Big.jpg|90px]] | ||
| + | | [[Image:Rote 53 Big.jpg|90px]] | ||
| + | |- | ||
| + | | <math>64\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_1^6 | ||
| + | & = & \text{p}_1^{\text{p}_1^1 \text{p}_2^1} | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_1^{\text{p}_1^1 \text{p}_{\text{p}_1^1}^1} | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}^{\text{p} \text{p}_{\text{p}}}\!</math> | ||
| + | | [[Image:Riff 64 Big.jpg|65px]] | ||
| + | | [[Image:Rote 64 Big.jpg|105px]] | ||
| + | |- | ||
| + | | <math>81\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_2^4 | ||
| + | & = & \text{p}_{\text{p}_1^1}^{\text{p}_1^2} | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_{\text{p}_1^1}^{\text{p}_1^{\text{p}_1^1}} | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}_{\text{p}}^{\text{p}^{\text{p}}}\!</math> | ||
| + | | [[Image:Riff 81 Big.jpg|65px]] | ||
| + | | [[Image:Rote 81 Big.jpg|105px]] | ||
| + | |- | ||
| + | | <math>128\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_1^7 | ||
| + | & = & \text{p}_1^{\text{p}_4^1} | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_1^{\text{p}_{\text{p}_1^2}^1} | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_1^{\text{p}_{\text{p}_1^{\text{p}_1^1}}^1} | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}^{\text{p}_{\text{p}^{\text{p}}}}\!</math> | ||
| + | | [[Image:Riff 128 Big.jpg|90px]] | ||
| + | | [[Image:Rote 128 Big.jpg|90px]] | ||
| + | |- | ||
| + | | <math>256\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_1^8 | ||
| + | & = & \text{p}_1^{\text{p}_1^3} | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_1^{\text{p}_1^{\text{p}_2^1}} | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_1^{\text{p}_1^{\text{p}_{\text{p}_1^1}^1}} | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}^{\text{p}^{\text{p}_{\text{p}}}}\!</math> | ||
| + | | [[Image:Riff 256 Big.jpg|90px]] | ||
| + | | [[Image:Rote 256 Big.jpg|90px]] | ||
| + | |- | ||
| + | | <math>512\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_1^9 | ||
| + | & = & \text{p}_1^{\text{p}_2^2} | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_1^{\text{p}_{\text{p}_1^1}^{\text{p}_1^1}} | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}^{\text{p}_{\text{p}}^{\text{p}}}\!</math> | ||
| + | | [[Image:Riff 512 Big.jpg|65px]] | ||
| + | | [[Image:Rote 512 Big.jpg|105px]] | ||
| + | |- | ||
| + | | <math>65536\!</math> | ||
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \text{p}_1^{16} | ||
| + | & = & \text{p}_1^{\text{p}_1^4} | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_1^{\text{p}_1^{\text{p}_1^2}} | ||
| + | \\[12pt] | ||
| + | & = & \text{p}_1^{\text{p}_1^{\text{p}_1^{\text{p}_1^1}}} | ||
| + | \end{array}</math> | ||
| + | | <math>\text{p}^{\text{p}^{\text{p}^{\text{p}}}}\!</math> | ||
| + | | [[Image:Riff 65536 Big.jpg|90px]] | ||
| + | | [[Image:Rote 65536 Big.jpg|115px]] | ||
| + | |} | ||
| + | |} | ||
| + | |||
| + | ===A062537=== | ||
| + | |||
| + | * '''Nodes in riff (rooted index-functional forest) for n.''' | ||
| + | |||
| + | * [http://oeis.org/A062537 OEIS Entry for A062537]. | ||
| + | |||
| + | {| align="center" border="1" cellpadding="10" | ||
| + | |+ style="height:25px" | <math>a(n) = \text{Number of Nodes in the Riff of}~ n</math> | ||
| + | | valign="bottom" | | ||
| + | <p> </p><br> | ||
| + | <p><math>1\!</math></p><br> | ||
| + | <p><math>a(1) ~=~ 0</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 2 Big.jpg|20px]]</p><br> | ||
| + | <p><math>\text{p}\!</math></p><br> | ||
| + | <p><math>a(2) ~=~ 1</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 3 Big.jpg|40px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p}\!</math></p><br> | ||
| + | <p><math>a(3) ~=~ 2</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 4 Big.jpg|40px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(4) ~=~ 2</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 5 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(5) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 6 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}}\!</math></p><br> | ||
| + | <p><math>a(6) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 7 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^{\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(7) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 8 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_{\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(8) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 9 Big.jpg|40px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(9) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 10 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_{\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(10) ~=~ 4</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 11 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p}_{\text{p}}}}\!</math></p><br> | ||
| + | <p><math>a(11) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 12 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_\text{p}\!</math></p><br> | ||
| + | <p><math>a(12) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 13 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p} \text{p}_{\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(13) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 14 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}^{\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(14) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 15 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(15) ~=~ 5</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 16 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}^{\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(16) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 17 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p}^{\text{p}}}}\!</math></p><br> | ||
| + | <p><math>a(17) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 18 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(18) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 19 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^{\text{p}_{\text{p}}}}\!</math></p><br> | ||
| + | <p><math>a(19) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 20 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_{\text{p}_{\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(20) ~=~ 5</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 21 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(21) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 22 Big.jpg|115px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(22) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 23 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(23) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 24 Big.jpg|115px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_\text{p}} \text{p}_\text{p}\!</math></p><br> | ||
| + | <p><math>a(24) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 25 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(25) ~=~ 4</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 26 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(26) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 27 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p}^{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(27) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 28 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(28) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 29 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(29) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 30 Big.jpg|115px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(30) ~=~ 6</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 31 Big.jpg|115px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p}_{\text{p}_\text{p}}}}\!</math></p><br> | ||
| + | <p><math>a(31) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 32 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(32) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 33 Big.jpg|115px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(33) ~=~ 6</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 34 Big.jpg|115px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(34) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 35 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(35) ~=~ 6</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 36 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_\text{p}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(36) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 37 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^\text{p} \text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(37) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 38 Big.jpg|115px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(38) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 39 Big.jpg|115px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(39) ~=~ 6</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 40 Big.jpg|135px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(40) ~=~ 6</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 41 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p} \text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(41) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 42 Big.jpg|115px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(42) ~=~ 6</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 43 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p} \text{p}_{\text{p}^\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(43) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 44 Big.jpg|115px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(44) ~=~ 6</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 45 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(45) ~=~ 6</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 46 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(46) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 47 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(47) ~=~ 6</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 48 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}^\text{p}} \text{p}_\text{p}\!</math></p><br> | ||
| + | <p><math>a(48) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 49 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^\text{p}}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(49) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 50 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_\text{p}}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(50) ~=~ 5</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 51 Big.jpg|115px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(51) ~=~ 6</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 52 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(52) ~=~ 6</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 53 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^{\text{p}^\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(53) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 54 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p}^{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(54) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 55 Big.jpg|115px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(55) ~=~ 7</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 56 Big.jpg|135px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(56) ~=~ 6</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 57 Big.jpg|115px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(57) ~=~ 6</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 58 Big.jpg|115px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(58) ~=~ 6</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 59 Big.jpg|115px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p}_{\text{p}^\text{p}}}}\!</math></p><br> | ||
| + | <p><math>a(59) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 60 Big.jpg|115px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(60) ~=~ 7</math></p> | ||
| + | |} | ||
| + | |||
| + | ===A062860=== | ||
| + | |||
| + | * '''Smallest j with n nodes in its riff (rooted index-functional forest).''' | ||
| + | |||
| + | * [http://oeis.org/A062860 OEIS Entry for A062860]. | ||
| + | |||
| + | {| align="center" border="1" cellpadding="10" | ||
| + | |+ style="height:25px" | <math>a(n) = \text{Least Integer}~ j ~\text{with}~ n ~\text{Nodes in Its Riff}</math> | ||
| + | | valign="bottom" | | ||
| + | <p> </p><br> | ||
| + | <p><math>1\!</math></p><br> | ||
| + | <p><math>a(0) ~=~ 1</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 2 Big.jpg|20px]]</p><br> | ||
| + | <p><math>\text{p}\!</math></p><br> | ||
| + | <p><math>a(1) ~=~ 2</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 3 Big.jpg|40px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p}\!</math></p><br> | ||
| + | <p><math>a(2) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 5 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(3) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 10 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_{\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(4) ~=~ 10</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 15 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(5) ~=~ 15</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 30 Big.jpg|115px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(6) ~=~ 30</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 55 Big.jpg|115px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(7) ~=~ 55</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 105 Big.jpg|115px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(8) ~=~ 105</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Riff 165 Big.jpg|135px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(9) ~=~ 165</math></p> | ||
| + | |} | ||
| + | |||
| + | ===A109301=== | ||
| + | |||
| + | * '''a(n) = rhig(n) = rote height in gammas of n, where the "rote" corresponding to a positive integer n is a graph derived from the primes factorization of n, as illustrated in the comments.''' | ||
| + | |||
| + | * [http://oeis.org/A109301 OEIS Entry for A109301]. | ||
| + | |||
| + | ; Example | ||
| + | |||
| + | : <math>802701 = 9 \cdot 89189 = \text{p}_2^2 \text{p}_{8638}^1</math> | ||
| + | |||
| + | : <math>\text{Writing}~ (\operatorname{prime}(i))^j ~\text{as}~ i\!:\!j, ~\text{we have:}</math> | ||
| + | |||
| + | : <math>\begin{array}{lllll} | ||
| + | 802701 | ||
| + | & = & 9 \cdot 89189 | ||
| + | & = & 2\!:\!2 ~~ 8638\!:\!1 | ||
| + | \\ | ||
| + | 8638 | ||
| + | & = & 2 \cdot 7 \cdot 617 | ||
| + | & = & 1\!:\!1 ~~ 4\!:\!1 ~~ 113\!:\!1 | ||
| + | \\ | ||
| + | 113 | ||
| + | & & | ||
| + | & = & 30\!:\!1 | ||
| + | \\ | ||
| + | 30 | ||
| + | & = & 2 \cdot 3 \cdot 5 | ||
| + | & = & 1\!:\!1 ~~ 2\!:\!1 ~~ 3\!:\!1 | ||
| + | \\ | ||
| + | 4 | ||
| + | & & | ||
| + | & = & 1\!:\!2 | ||
| + | \\ | ||
| + | 3 | ||
| + | & & | ||
| + | & = & 2\!:\!1 | ||
| + | \\ | ||
| + | 2 | ||
| + | & & | ||
| + | & = & 1\!:\!1 | ||
| + | \end{array}</math> | ||
| + | |||
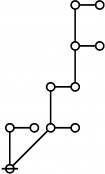
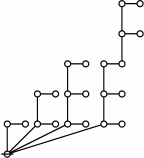
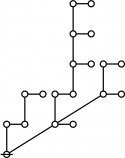
| + | : <math>\text{So the rote of 802701 is the following graph:}\!</math> | ||
| + | |||
| + | :{| border="1" cellpadding="20" | ||
| + | | [[Image:Rote 802701 Big.jpg|330px]] | ||
| + | |} | ||
| + | |||
| + | : <math>\text{By inspection, the rote height of 802701 is 6.}\!</math> | ||
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" border="1" cellpadding="6" | ||
| + | |+ style="height:25px" | <math>a(n) = \text{Rote Height of}~ n</math> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 1 Big.jpg|20px]]</p><br> | ||
| + | <p><math>1\!</math></p><br> | ||
| + | <p><math>a(1) ~=~ 0</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 2 Big.jpg|40px]]</p><br> | ||
| + | <p><math>\text{p}\!</math></p><br> | ||
| + | <p><math>a(2) ~=~ 1</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 3 Big.jpg|40px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p}\!</math></p><br> | ||
| + | <p><math>a(3) ~=~ 2</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 4 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(4) ~=~ 2</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 5 Big.jpg|40px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(5) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 6 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p}\!</math></p><br> | ||
| + | <p><math>a(6) ~=~ 2</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 7 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(7) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 8 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(8) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 9 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(9) ~=~ 2</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 10 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(10) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 11 Big.jpg|40px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(11) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 12 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_\text{p}\!</math></p><br> | ||
| + | <p><math>a(12) ~=~ 2</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 13 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p} \text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(13) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 14 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(14) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 15 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(15) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 16 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(16) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 17 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p}^\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(17) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 18 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(18) ~=~ 2</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 19 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(19) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 20 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(20) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 21 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(21) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 22 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(22) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 23 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(23) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 24 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_\text{p}} \text{p}_\text{p}\!</math></p><br> | ||
| + | <p><math>a(24) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 25 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(25) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 26 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(26) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 27 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p}^{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(27) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 28 Big.jpg|130px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(28) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 29 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(29) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 30 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(30) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 31 Big.jpg|40px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p}_{\text{p}_\text{p}}}}\!</math></p><br> | ||
| + | <p><math>a(31) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 32 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(32) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 33 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(33) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 34 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(34) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 35 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(35) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 36 Big.jpg|145px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_\text{p}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(36) ~=~ 2</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 37 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^\text{p} \text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(37) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 38 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(38) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 39 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(39) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 40 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(40) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 41 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p} \text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(41) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 42 Big.jpg|145px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(42) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 43 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p} \text{p}_{\text{p}^\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(43) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 44 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(44) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 45 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(45) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 46 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(46) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 47 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(47) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 48 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}^\text{p}} \text{p}_\text{p}\!</math></p><br> | ||
| + | <p><math>a(48) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 49 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^\text{p}}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(49) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 50 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_\text{p}}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(50) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 51 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(51) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 52 Big.jpg|145px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(52) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 53 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^{\text{p}^\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(53) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 54 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p}^{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(54) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 55 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(55) ~=~ 4</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 56 Big.jpg|130px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(56) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 57 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(57) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 58 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(58) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 59 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p}_{\text{p}^\text{p}}}}\!</math></p><br> | ||
| + | <p><math>a(59) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 60 Big.jpg|155px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(60) ~=~ 3</math></p> | ||
| + | |} | ||
| + | |||
| + | ==Miscellaneous Examples== | ||
| + | |||
| + | {| align="center" border="1" width="96%" | ||
| + | |+ style="height:24px" | <math>\text{Integers, Riffs, Rotes}\!</math> | ||
| + | |- style="height:50px; background:#f0f0ff" | ||
| + | | | ||
| + | {| cellpadding="12" style="background:#f0f0ff; text-align:center; width:100%" | ||
| + | | width="10%" | <math>\text{Integer}\!</math> | ||
| + | | width="45%" | <math>\text{Riff}\!</math> | ||
| + | | width="45%" | <math>\text{Rote}\!</math> | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| cellpadding="12" style="text-align:center; width:100%" | ||
| + | | width="10%" | <math>1\!</math> | ||
| + | | width="45%" | | ||
| + | | width="45%" | [[Image:Rote 1 Big.jpg|15px]] | ||
| + | |- | ||
| + | | <math>2\!</math> | ||
| + | | [[Image:Riff 2 Big.jpg|15px]] | ||
| + | | [[Image:Rote 2 Big.jpg|30px]] | ||
| + | |- | ||
| + | | <math>3\!</math> | ||
| + | | [[Image:Riff 3 Big.jpg|30px]] | ||
| + | | [[Image:Rote 3 Big.jpg|30px]] | ||
| + | |- | ||
| + | | <math>4\!</math> | ||
| + | | [[Image:Riff 4 Big.jpg|30px]] | ||
| + | | [[Image:Rote 4 Big.jpg|48px]] | ||
| + | |- | ||
| + | | <math>360\!</math> | ||
| + | | [[Image:Riff 360 Big.jpg|120px]] | ||
| + | | [[Image:Rote 360 Big.jpg|135px]] | ||
| + | |- | ||
| + | | <math>2010\!</math> | ||
| + | | [[Image:Riff 2010 Big.jpg|138px]] | ||
| + | | [[Image:Rote 2010 Big.jpg|144px]] | ||
| + | |- | ||
| + | | <math>2011\!</math> | ||
| + | | [[Image:Riff 2011 Big.jpg|84px]] | ||
| + | | [[Image:Rote 2011 Big.jpg|120px]] | ||
| + | |- | ||
| + | | <math>2012\!</math> | ||
| + | | [[Image:Riff 2012 Big.jpg|100px]] | ||
| + | | [[Image:Rote 2012 Big.jpg|125px]] | ||
| + | |- | ||
| + | | <math>2500\!</math> | ||
| + | | [[Image:Riff 2500 Big.jpg|66px]] | ||
| + | | [[Image:Rote 2500 Big.jpg|125px]] | ||
| + | |- | ||
| + | | <math>802701\!</math> | ||
| + | | [[Image:Riff 802701 Big.jpg|156px]] | ||
| + | | [[Image:Rote 802701 Big.jpg|245px]] | ||
| + | |- | ||
| + | | <math>123456789\!</math> | ||
| + | | [[Image:Riff 123456789 Big.jpg|162px]] | ||
| + | | [[Image:Rote 123456789 Big.jpg|256px]] | ||
| + | |} | ||
|} | |} | ||
Latest revision as of 22:00, 30 January 2016
Idea
Let \(\text{p}_i\!\) be the \(i^\text{th}\!\) prime, where the positive integer \(i\!\) is called the index of the prime \(\text{p}_i\!\) and the indices are taken in such a way that \(\text{p}_1 = 2.\!\) Thus the sequence of primes begins as follows:
|
\(\begin{matrix} \text{p}_1 = 2, & \text{p}_2 = 3, & \text{p}_3 = 5, & \text{p}_4 = 7, & \text{p}_5 = 11, & \text{p}_6 = 13, & \text{p}_7 = 17, & \text{p}_8 = 19, & \ldots \end{matrix}\) |
The prime factorization of a positive integer \(n\!\) can be written in the following form:
| \(n ~=~ \prod_{k = 1}^{\ell} \text{p}_{i(k)}^{j(k)},\!\) |
where \(\text{p}_{i(k)}^{j(k)}\!\) is the \(k^\text{th}\!\) prime power in the factorization and \(\ell\!\) is the number of distinct prime factors dividing \(n.\!\) The factorization of \(1\!\) is defined as \(1\!\) in accord with the convention that an empty product is equal to \(1.\!\)
Let \(I(n)\!\) be the set of indices of primes that divide \(n\!\) and let \(j(i, n)\!\) be the number of times that \(\text{p}_i\!\) divides \(n.\!\) Then the prime factorization of \(n\!\) can be written in the following alternative form:
| \(n ~=~ \prod_{i \in I(n)} \text{p}_{i}^{j(i, n)}.\!\) |
For example:
|
\(\begin{matrix} 123456789 & = & 3^2 \cdot 3607 \cdot 3803 & = & \text{p}_2^2 \text{p}_{504}^1 \text{p}_{529}^1. \end{matrix}\) |
Each index \(i\!\) and exponent \(j\!\) appearing in the prime factorization of a positive integer \(n\!\) is itself a positive integer, and thus has a prime factorization of its own.
Continuing with the same example, the index \(504\!\) has the factorization \(2^3 \cdot 3^2 \cdot 7 = \text{p}_1^3 \text{p}_2^2 \text{p}_4^1\!\) and the index \(529\!\) has the factorization \({23}^2 = \text{p}_9^2.\!\) Taking this information together with previously known factorizations allows the following replacements to be made in the expression above:
|
\(\begin{array}{rcl} 2 & \mapsto & \text{p}_1^1 \'"`UNIQ-MathJax1-QINU`"' '"`UNIQ-MathJax2-QINU`"' '"`UNIQ-MathJax3-QINU`"' '"`UNIQ-MathJax4-QINU`"' :{| border="1" cellpadding="20" | [[Image:Rote 802701 Big.jpg|330px]] |} '"`UNIQ-MathJax5-QINU`"' <br> {| align="center" border="1" cellpadding="6" |+ style="height:25px" | \(a(n) = \text{Rote Height of}~ n\) |
\(1\!\) \(a(1) ~=~ 0\) |
\(\text{p}\!\) \(a(2) ~=~ 1\) |
\(\text{p}_\text{p}\!\) \(a(3) ~=~ 2\) |
\(\text{p}^\text{p}\!\) \(a(4) ~=~ 2\) |
\(\text{p}_{\text{p}_\text{p}}\!\) \(a(5) ~=~ 3\) |
|
\(\text{p} \text{p}_\text{p}\!\) \(a(6) ~=~ 2\) |
\(\text{p}_{\text{p}^\text{p}}\!\) \(a(7) ~=~ 3\) |
\(\text{p}^{\text{p}_\text{p}}\!\) \(a(8) ~=~ 3\) |
\(\text{p}_\text{p}^\text{p}\!\) \(a(9) ~=~ 2\) |
\(\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(10) ~=~ 3\) | |
|
\(\text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(11) ~=~ 4\) |
\(\text{p}^\text{p} \text{p}_\text{p}\!\) \(a(12) ~=~ 2\) |
\(\text{p}_{\text{p} \text{p}_\text{p}}\!\) \(a(13) ~=~ 3\) |
\(\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(a(14) ~=~ 3\) |
\(\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(15) ~=~ 3\) | |
|
\(\text{p}^{\text{p}^\text{p}}\!\) \(a(16) ~=~ 3\) |
\(\text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(a(17) ~=~ 4\) |
\(\text{p} \text{p}_\text{p}^\text{p}\!\) \(a(18) ~=~ 2\) |
\(\text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(a(19) ~=~ 4\) |
\(\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(20) ~=~ 3\) | |
|
\(\text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(a(21) ~=~ 3\) |
\(\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(22) ~=~ 4\) |
\(\text{p}_{\text{p}_\text{p}^\text{p}}\!\) \(a(23) ~=~ 3\) |
\(\text{p}^{\text{p}_\text{p}} \text{p}_\text{p}\!\) \(a(24) ~=~ 3\) |
\(\text{p}_{\text{p}_\text{p}}^\text{p}\!\) \(a(25) ~=~ 3\) | |
|
\(\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(a(26) ~=~ 3\) |
\(\text{p}_\text{p}^{\text{p}_\text{p}}\!\) \(a(27) ~=~ 3\) |
\(\text{p}^\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(a(28) ~=~ 3\) |
\(\text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(a(29) ~=~ 4\) |
\(\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(30) ~=~ 3\) | |
|
\(\text{p}_{\text{p}_{\text{p}_{\text{p}_\text{p}}}}\!\) \(a(31) ~=~ 5\) |
\(\text{p}^{\text{p}_{\text{p}_\text{p}}}\!\) \(a(32) ~=~ 4\) |
\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(33) ~=~ 4\) |
\(\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(a(34) ~=~ 4\) |
\(\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!\) \(a(35) ~=~ 3\) | |
|
\(\text{p}^\text{p} \text{p}_\text{p}^\text{p}\!\) \(a(36) ~=~ 2\) |
\(\text{p}_{\text{p}^\text{p} \text{p}_\text{p}}\!\) \(a(37) ~=~ 3\) |
\(\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(a(38) ~=~ 4\) |
\(\text{p}_\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(a(39) ~=~ 3\) |
\(\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}_\text{p}}\!\) \(a(40) ~=~ 3\) | |
|
\(\text{p}_{\text{p}_{\text{p} \text{p}_\text{p}}}\!\) \(a(41) ~=~ 4\) |
\(\text{p} \text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(a(42) ~=~ 3\) |
\(\text{p}_{\text{p} \text{p}_{\text{p}^\text{p}}}\!\) \(a(43) ~=~ 4\) |
\(\text{p}^\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(44) ~=~ 4\) |
\(\text{p}_\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(45) ~=~ 3\) | |
|
\(\text{p} \text{p}_{\text{p}_\text{p}^\text{p}}\!\) \(a(46) ~=~ 3\) |
\(\text{p}_{\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(a(47) ~=~ 4\) |
\(\text{p}^{\text{p}^\text{p}} \text{p}_\text{p}\!\) \(a(48) ~=~ 3\) |
\(\text{p}_{\text{p}^\text{p}}^\text{p}\!\) \(a(49) ~=~ 3\) |
\(\text{p} \text{p}_{\text{p}_\text{p}}^\text{p}\!\) \(a(50) ~=~ 3\) | |
|
\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(a(51) ~=~ 4\) |
\(\text{p}^\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(a(52) ~=~ 3\) |
\(\text{p}_{\text{p}^{\text{p}^\text{p}}}\!\) \(a(53) ~=~ 4\) |
\(\text{p} \text{p}_\text{p}^{\text{p}_\text{p}}\!\) \(a(54) ~=~ 3\) |
\(\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(55) ~=~ 4\) | |
|
\(\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!\) \(a(56) ~=~ 3\) |
\(\text{p}_\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(a(57) ~=~ 4\) |
\(\text{p} \text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(a(58) ~=~ 4\) |
\(\text{p}_{\text{p}_{\text{p}_{\text{p}^\text{p}}}}\!\) \(a(59) ~=~ 5\) |
\(\text{p}^\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(60) ~=~ 3\) |
Miscellaneous Examples
| |||||||||||||||||||||||||||||||||
|