Difference between revisions of "Directory:Jon Awbrey/Papers/Riffs and Rotes"
Jon Awbrey (talk | contribs) |
Jon Awbrey (talk | contribs) |
||
| Line 1,240: | Line 1,240: | ||
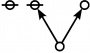
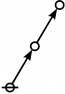
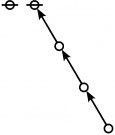
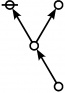
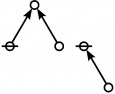
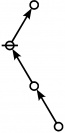
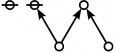
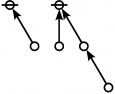
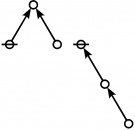
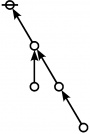
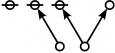
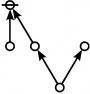
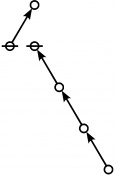
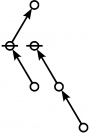
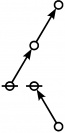
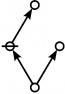
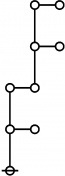
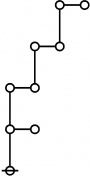
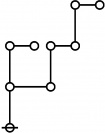
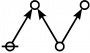
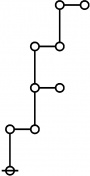
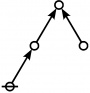
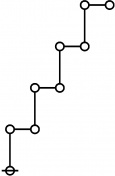
<p><math>\text{p}_\text{p} \text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | <p><math>\text{p}_\text{p} \text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
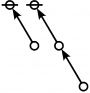
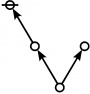
<p><math>a(9) ~=~ 165</math></p> | <p><math>a(9) ~=~ 165</math></p> | ||
| + | |} | ||
| + | |||
| + | ===A109301=== | ||
| + | |||
| + | * '''a(n) = rhig(n) = rote height in gammas of n, where the "rote" corresponding to a positive integer n is a graph derived from the primes factorization of n, as illustrated in the comments.''' | ||
| + | |||
| + | * [http://oeis.org/wiki/A109301 OEIS Wiki Entry for A109301]. | ||
| + | |||
| + | {| align="center" border="1" cellpadding="6" | ||
| + | |+ style="height:25px" | <math>a(n) = \text{Rote Height of}~ n</math> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 1 Big.jpg|20px]]</p><br> | ||
| + | <p><math>1\!</math></p><br> | ||
| + | <p><math>a(1) ~=~ 0</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 2 Big.jpg|40px]]</p><br> | ||
| + | <p><math>\text{p}\!</math></p><br> | ||
| + | <p><math>a(2) ~=~ 1</math></p> | ||
| + | | valign="bottom" | | ||
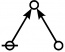
| + | <p>[[Image:Rote 3 Big.jpg|40px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p}\!</math></p><br> | ||
| + | <p><math>a(3) ~=~ 2</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 4 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(4) ~=~ 2</math></p> | ||
| + | | valign="bottom" | | ||
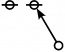
| + | <p>[[Image:Rote 5 Big.jpg|40px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(5) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 6 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p}\!</math></p><br> | ||
| + | <p><math>a(6) ~=~ 2</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 7 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(7) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 8 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(8) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
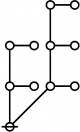
| + | <p>[[Image:Rote 9 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(9) ~=~ 2</math></p> | ||
| + | | valign="bottom" | | ||
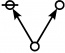
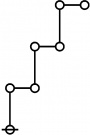
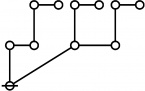
| + | <p>[[Image:Rote 10 Big.jpg|80px]]</p><br> | ||
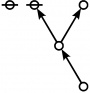
| + | <p><math>\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(10) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
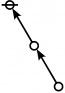
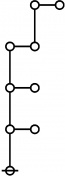
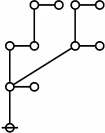
| + | <p>[[Image:Rote 11 Big.jpg|40px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(11) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
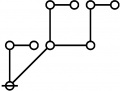
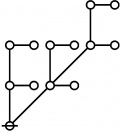
| + | <p>[[Image:Rote 12 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_\text{p}\!</math></p><br> | ||
| + | <p><math>a(12) ~=~ 2</math></p> | ||
| + | | valign="bottom" | | ||
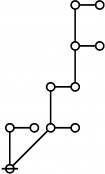
| + | <p>[[Image:Rote 13 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p} \text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(13) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 14 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(14) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 15 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(15) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 16 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(16) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 17 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p}^\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(17) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 18 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(18) ~=~ 2</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 19 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(19) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 20 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(20) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 21 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(21) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 22 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(22) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 23 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(23) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 24 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_\text{p}} \text{p}_\text{p}\!</math></p><br> | ||
| + | <p><math>a(24) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 25 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(25) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 26 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(26) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 27 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p}^{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(27) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 28 Big.jpg|130px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(28) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 29 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(29) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 30 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(30) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 31 Big.jpg|40px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p}_{\text{p}_\text{p}}}}\!</math></p><br> | ||
| + | <p><math>a(31) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 32 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(32) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 33 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(33) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 34 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(34) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 35 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(35) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 36 Big.jpg|145px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_\text{p}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(36) ~=~ 2</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 37 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^\text{p} \text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(37) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 38 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(38) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 39 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(39) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 40 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(40) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 41 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p} \text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(41) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 42 Big.jpg|145px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(42) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 43 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p} \text{p}_{\text{p}^\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(43) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 44 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(44) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 45 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(45) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 46 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(46) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 47 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(47) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 48 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}^\text{p}} \text{p}_\text{p}\!</math></p><br> | ||
| + | <p><math>a(48) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 49 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^\text{p}}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(49) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 50 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p}_\text{p}}^\text{p}\!</math></p><br> | ||
| + | <p><math>a(50) ~=~ 3</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 51 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(51) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 52 Big.jpg|145px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(52) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 53 Big.jpg|90px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}^{\text{p}^\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(53) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 54 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_\text{p}^{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(54) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 55 Big.jpg|80px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(55) ~=~ 4</math></p> | ||
| + | |- | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 56 Big.jpg|130px]]</p><br> | ||
| + | <p><math>\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!</math></p><br> | ||
| + | <p><math>a(56) ~=~ 3</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 57 Big.jpg|105px]]</p><br> | ||
| + | <p><math>\text{p}_\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(57) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 58 Big.jpg|120px]]</p><br> | ||
| + | <p><math>\text{p} \text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!</math></p><br> | ||
| + | <p><math>a(58) ~=~ 4</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 59 Big.jpg|65px]]</p><br> | ||
| + | <p><math>\text{p}_{\text{p}_{\text{p}_{\text{p}^\text{p}}}}\!</math></p><br> | ||
| + | <p><math>a(59) ~=~ 5</math></p> | ||
| + | | valign="bottom" | | ||
| + | <p>[[Image:Rote 60 Big.jpg|155px]]</p><br> | ||
| + | <p><math>\text{p}^\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br> | ||
| + | <p><math>a(60) ~=~ 3</math></p> | ||
|} | |} | ||
Revision as of 18:34, 23 January 2010
Riffs in Numerical Order
|
\(1\!\) \(\begin{array}{l} \varnothing \\ 1 \end{array}\) |
\(\text{p}\!\) \(\begin{array}{l} 1\!:\!1 \\ 2 \end{array}\) |
\(\text{p}_\text{p}\!\) \(\begin{array}{l} 2\!:\!1 \\ 3 \end{array}\) |
\(\text{p}^\text{p}\!\) \(\begin{array}{l} 1\!:\!2 \\ 4 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 3\!:\!1 \\ 5 \end{array}\) |
|
\(\text{p} \text{p}_\text{p}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 \\ 6 \end{array}\) |
\(\text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 4\!:\!1 \\ 7 \end{array}\) |
\(\text{p}^{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!3 \\ 8 \end{array}\) |
\(\text{p}_\text{p}^\text{p}\!\) \(\begin{array}{l} 2\!:\!2 \\ 9 \end{array}\) |
\(\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 3\!:\!1 \\ 10 \end{array}\) |
|
\(\text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 5\!:\!1 \\ 11 \end{array}\) |
\(\text{p}^\text{p} \text{p}_\text{p}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 \\ 12 \end{array}\) |
\(\text{p}_{\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 6\!:\!1 \\ 13 \end{array}\) |
\(\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 4\!:\!1 \\ 14 \end{array}\) |
\(\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 3\!:\!1 \\ 15 \end{array}\) |
|
\(\text{p}^{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!4 \\ 16 \end{array}\) |
\(\text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 7\!:\!1 \\ 17 \end{array}\) |
\(\text{p} \text{p}_\text{p}^\text{p}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!2 \\ 18 \end{array}\) |
\(\text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 8\!:\!1 \\ 19 \end{array}\) |
\(\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 3\!:\!1 \\ 20 \end{array}\) |
|
\(\text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 4\!:\!1 \\ 21 \end{array}\) |
\(\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 5\!:\!1 \\ 22 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}^\text{p}}\!\) \(\begin{array}{l} 9\!:\!1 \\ 23 \end{array}\) |
\(\text{p}^{\text{p}_\text{p}} \text{p}_\text{p}\!\) \(\begin{array}{l} 1\!:\!3 ~~ 2\!:\!1 \\ 24 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}}^\text{p}\!\) \(\begin{array}{l} 3\!:\!2 \\ 25 \end{array}\) |
|
\(\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 6\!:\!1 \\ 26 \end{array}\) |
\(\text{p}_\text{p}^{\text{p}_\text{p}}\!\) \(\begin{array}{l} 2\!:\!3 \\ 27 \end{array}\) |
\(\text{p}^\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 4\!:\!1 \\ 28 \end{array}\) |
\(\text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 10\!:\!1 \\ 29 \end{array}\) |
\(\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 30 \end{array}\) |
|
\(\text{p}_{\text{p}_{\text{p}_{\text{p}_\text{p}}}}\!\) \(\begin{array}{l} 11\!:\!1 \\ 31 \end{array}\) |
\(\text{p}^{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!5 \\ 32 \end{array}\) |
\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 5\!:\!1 \\ 33 \end{array}\) |
\(\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 7\!:\!1 \\ 34 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 3\!:\!1 ~~ 4\!:\!1 \\ 35 \end{array}\) |
|
\(\text{p}^\text{p} \text{p}_\text{p}^\text{p}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 2\!:\!2 \\ 36 \end{array}\) |
\(\text{p}_{\text{p}^\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 12\!:\!1 \\ 37 \end{array}\) |
\(\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 8\!:\!1 \\ 38 \end{array}\) |
\(\text{p}_\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 6\!:\!1 \\ 39 \end{array}\) |
\(\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!3 ~~ 3\!:\!1 \\ 40 \end{array}\) |
|
\(\text{p}_{\text{p}_{\text{p} \text{p}_\text{p}}}\!\) \(\begin{array}{l} 13\!:\!1 \\ 41 \end{array}\) |
\(\text{p} \text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 ~~ 4\!:\!1 \\ 42 \end{array}\) |
\(\text{p}_{\text{p} \text{p}_{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 14\!:\!1 \\ 43 \end{array}\) |
\(\text{p}^\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 5\!:\!1 \\ 44 \end{array}\) |
\(\text{p}_\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 2\!:\!2 ~~ 3\!:\!1 \\ 45 \end{array}\) |
|
\(\text{p} \text{p}_{\text{p}_\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 9\!:\!1 \\ 46 \end{array}\) |
\(\text{p}_{\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 15\!:\!1 \\ 47 \end{array}\) |
\(\text{p}^{\text{p}^\text{p}} \text{p}_\text{p}\!\) \(\begin{array}{l} 1\!:\!4 ~~ 2\!:\!1 \\ 48 \end{array}\) |
\(\text{p}_{\text{p}^\text{p}}^\text{p}\!\) \(\begin{array}{l} 4\!:\!2 \\ 49 \end{array}\) |
\(\text{p} \text{p}_{\text{p}_\text{p}}^\text{p}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 3\!:\!2 \\ 50 \end{array}\) |
|
\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 7\!:\!1 \\ 51 \end{array}\) |
\(\text{p}^\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 6\!:\!1 \\ 52 \end{array}\) |
\(\text{p}_{\text{p}^{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 16\!:\!1 \\ 53 \end{array}\) |
\(\text{p} \text{p}_\text{p}^{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!3 \\ 54 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 3\!:\!1 ~~ 5\!:\!1 \\ 55 \end{array}\) |
|
\(\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!3 ~~ 4\!:\!1 \\ 56 \end{array}\) |
\(\text{p}_\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 8\!:\!1 \\ 57 \end{array}\) |
\(\text{p} \text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 10\!:\!1 \\ 58 \end{array}\) |
\(\text{p}_{\text{p}_{\text{p}_{\text{p}^\text{p}}}}\!\) \(\begin{array}{l} 17\!:\!1 \\ 59 \end{array}\) |
\(\text{p}^\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 60 \end{array}\) |
Rotes in Numerical Order
|
\(1\!\) \(\begin{array}{l} \varnothing \\ 1 \end{array}\) |
\(\text{p}\!\) \(\begin{array}{l} 1\!:\!1 \\ 2 \end{array}\) |
\(\text{p}_\text{p}\!\) \(\begin{array}{l} 2\!:\!1 \\ 3 \end{array}\) |
\(\text{p}^\text{p}\!\) \(\begin{array}{l} 1\!:\!2 \\ 4 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 3\!:\!1 \\ 5 \end{array}\) |
|
\(\text{p} \text{p}_\text{p}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 \\ 6 \end{array}\) |
\(\text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 4\!:\!1 \\ 7 \end{array}\) |
\(\text{p}^{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!3 \\ 8 \end{array}\) |
\(\text{p}_\text{p}^\text{p}\!\) \(\begin{array}{l} 2\!:\!2 \\ 9 \end{array}\) |
\(\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 3\!:\!1 \\ 10 \end{array}\) |
|
\(\text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 5\!:\!1 \\ 11 \end{array}\) |
\(\text{p}^\text{p} \text{p}_\text{p}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 \\ 12 \end{array}\) |
\(\text{p}_{\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 6\!:\!1 \\ 13 \end{array}\) |
\(\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 4\!:\!1 \\ 14 \end{array}\) |
\(\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 3\!:\!1 \\ 15 \end{array}\) |
|
\(\text{p}^{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!4 \\ 16 \end{array}\) |
\(\text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 7\!:\!1 \\ 17 \end{array}\) |
\(\text{p} \text{p}_\text{p}^\text{p}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!2 \\ 18 \end{array}\) |
\(\text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 8\!:\!1 \\ 19 \end{array}\) |
\(\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 3\!:\!1 \\ 20 \end{array}\) |
|
\(\text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 4\!:\!1 \\ 21 \end{array}\) |
\(\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 5\!:\!1 \\ 22 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}^\text{p}}\!\) \(\begin{array}{l} 9\!:\!1 \\ 23 \end{array}\) |
\(\text{p}^{\text{p}_\text{p}} \text{p}_\text{p}\!\) \(\begin{array}{l} 1\!:\!3 ~~ 2\!:\!1 \\ 24 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}}^\text{p}\!\) \(\begin{array}{l} 3\!:\!2 \\ 25 \end{array}\) |
|
\(\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 6\!:\!1 \\ 26 \end{array}\) |
\(\text{p}_\text{p}^{\text{p}_\text{p}}\!\) \(\begin{array}{l} 2\!:\!3 \\ 27 \end{array}\) |
\(\text{p}^\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 4\!:\!1 \\ 28 \end{array}\) |
\(\text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 10\!:\!1 \\ 29 \end{array}\) |
\(\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 30 \end{array}\) |
|
\(\text{p}_{\text{p}_{\text{p}_{\text{p}_\text{p}}}}\!\) \(\begin{array}{l} 11\!:\!1 \\ 31 \end{array}\) |
\(\text{p}^{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!5 \\ 32 \end{array}\) |
\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 5\!:\!1 \\ 33 \end{array}\) |
\(\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 7\!:\!1 \\ 34 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 3\!:\!1 ~~ 4\!:\!1 \\ 35 \end{array}\) |
|
\(\text{p}^\text{p} \text{p}_\text{p}^\text{p}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 2\!:\!2 \\ 36 \end{array}\) |
\(\text{p}_{\text{p}^\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 12\!:\!1 \\ 37 \end{array}\) |
\(\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 8\!:\!1 \\ 38 \end{array}\) |
\(\text{p}_\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 6\!:\!1 \\ 39 \end{array}\) |
\(\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!3 ~~ 3\!:\!1 \\ 40 \end{array}\) |
|
\(\text{p}_{\text{p}_{\text{p} \text{p}_\text{p}}}\!\) \(\begin{array}{l} 13\!:\!1 \\ 41 \end{array}\) |
\(\text{p} \text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 ~~ 4\!:\!1 \\ 42 \end{array}\) |
\(\text{p}_{\text{p} \text{p}_{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 14\!:\!1 \\ 43 \end{array}\) |
\(\text{p}^\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 5\!:\!1 \\ 44 \end{array}\) |
\(\text{p}_\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 2\!:\!2 ~~ 3\!:\!1 \\ 45 \end{array}\) |
|
\(\text{p} \text{p}_{\text{p}_\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 9\!:\!1 \\ 46 \end{array}\) |
\(\text{p}_{\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 15\!:\!1 \\ 47 \end{array}\) |
\(\text{p}^{\text{p}^\text{p}} \text{p}_\text{p}\!\) \(\begin{array}{l} 1\!:\!4 ~~ 2\!:\!1 \\ 48 \end{array}\) |
\(\text{p}_{\text{p}^\text{p}}^\text{p}\!\) \(\begin{array}{l} 4\!:\!2 \\ 49 \end{array}\) |
\(\text{p} \text{p}_{\text{p}_\text{p}}^\text{p}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 3\!:\!2 \\ 50 \end{array}\) |
|
\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 7\!:\!1 \\ 51 \end{array}\) |
\(\text{p}^\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 6\!:\!1 \\ 52 \end{array}\) |
\(\text{p}_{\text{p}^{\text{p}^\text{p}}}\!\) \(\begin{array}{l} 16\!:\!1 \\ 53 \end{array}\) |
\(\text{p} \text{p}_\text{p}^{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!3 \\ 54 \end{array}\) |
\(\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 3\!:\!1 ~~ 5\!:\!1 \\ 55 \end{array}\) |
|
\(\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!\) \(\begin{array}{l} 1\!:\!3 ~~ 4\!:\!1 \\ 56 \end{array}\) |
\(\text{p}_\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 2\!:\!1 ~~ 8\!:\!1 \\ 57 \end{array}\) |
\(\text{p} \text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(\begin{array}{l} 1\!:\!1 ~~ 10\!:\!1 \\ 58 \end{array}\) |
\(\text{p}_{\text{p}_{\text{p}_{\text{p}^\text{p}}}}\!\) \(\begin{array}{l} 17\!:\!1 \\ 59 \end{array}\) |
\(\text{p}^\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 60 \end{array}\) |
Selected Sequences
A061396
- Number of "rooted index-functional forests" (Riffs) on n nodes.
- Number of "rooted odd trees with only exponent symmetries" (Rotes) on 2n+1 nodes.
A062504
- Triangle in which k-th row lists natural number values for the collection of riffs with k nodes.
|
\(\begin{array}{l|l|r} k & P_k = \{ n : \operatorname{riff}(n) ~\text{has}~ k ~\text{nodes} \} = \{ n : \operatorname{rote}(n) ~\text{has}~ 2k + 1 ~\text{nodes} \} & |P_k| \\[10pt] 0 & \{ 1 \} & 1 \\ 1 & \{ 2 \} & 1 \\ 2 & \{ 3, 4 \} & 2 \\ 3 & \{ 5, 6, 7, 8, 9, 16 \} & 6 \\ 4 & \{ 10, 11, 12, 13, 14, 17, 18, 19, 23, 25, 27, 32, 49, 53, 64, 81, 128, 256, 512, 65536 \} & 20 \end{array}\) |
A062537
- Nodes in riff (rooted index-functional forest) for n.
|
\(1\!\) \(a(1) ~=~ 0\) |
\(\text{p}\!\) \(a(2) ~=~ 1\) |
\(\text{p}_\text{p}\!\) \(a(3) ~=~ 2\) |
\(\text{p}^\text{p}\!\) \(a(4) ~=~ 2\) |
\(\text{p}_{\text{p}_{\text{p}}}\!\) \(a(5) ~=~ 3\) |
|
\(\text{p} \text{p}_{\text{p}}\!\) \(a(6) ~=~ 3\) |
\(\text{p}_{\text{p}^{\text{p}}}\!\) \(a(7) ~=~ 3\) |
\(\text{p}^{\text{p}_{\text{p}}}\!\) \(a(8) ~=~ 3\) |
\(\text{p}_\text{p}^\text{p}\!\) \(a(9) ~=~ 3\) |
\(\text{p} \text{p}_{\text{p}_{\text{p}}}\!\) \(a(10) ~=~ 4\) |
|
\(\text{p}_{\text{p}_{\text{p}_{\text{p}}}}\!\) \(a(11) ~=~ 4\) |
\(\text{p}^\text{p} \text{p}_\text{p}\!\) \(a(12) ~=~ 4\) |
\(\text{p}_{\text{p} \text{p}_{\text{p}}}\!\) \(a(13) ~=~ 4\) |
\(\text{p} \text{p}_{\text{p}^{\text{p}}}\!\) \(a(14) ~=~ 4\) |
\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}}}\!\) \(a(15) ~=~ 5\) |
|
\(\text{p}^{\text{p}^{\text{p}}}\!\) \(a(16) ~=~ 3\) |
\(\text{p}_{\text{p}_{\text{p}^{\text{p}}}}\!\) \(a(17) ~=~ 4\) |
\(\text{p} \text{p}_\text{p}^\text{p}\!\) \(a(18) ~=~ 4\) |
\(\text{p}_{\text{p}^{\text{p}_{\text{p}}}}\!\) \(a(19) ~=~ 4\) |
\(\text{p}^\text{p} \text{p}_{\text{p}_{\text{p}}}\!\) \(a(20) ~=~ 5\) |
|
\(\text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(a(21) ~=~ 5\) |
\(\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(22) ~=~ 5\) |
\(\text{p}_{\text{p}_\text{p}^\text{p}}\!\) \(a(23) ~=~ 4\) |
\(\text{p}^{\text{p}_\text{p}} \text{p}_\text{p}\!\) \(a(24) ~=~ 5\) |
\(\text{p}_{\text{p}_\text{p}}^\text{p}\!\) \(a(25) ~=~ 4\) |
|
\(\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(a(26) ~=~ 5\) |
\(\text{p}_\text{p}^{\text{p}_\text{p}}\!\) \(a(27) ~=~ 4\) |
\(\text{p}^\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(a(28) ~=~ 5\) |
\(\text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(a(29) ~=~ 5\) |
\(\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(30) ~=~ 6\) |
|
\(\text{p}_{\text{p}_{\text{p}_{\text{p}_\text{p}}}}\!\) \(a(31) ~=~ 5\) |
\(\text{p}^{\text{p}_{\text{p}_\text{p}}}\!\) \(a(32) ~=~ 4\) |
\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(33) ~=~ 6\) |
\(\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(a(34) ~=~ 5\) |
\(\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!\) \(a(35) ~=~ 6\) |
|
\(\text{p}^\text{p} \text{p}_\text{p}^\text{p}\!\) \(a(36) ~=~ 5\) |
\(\text{p}_{\text{p}^\text{p} \text{p}_\text{p}}\!\) \(a(37) ~=~ 5\) |
\(\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(a(38) ~=~ 5\) |
\(\text{p}_\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(a(39) ~=~ 6\) |
\(\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}_\text{p}}\!\) \(a(40) ~=~ 6\) |
|
\(\text{p}_{\text{p}_{\text{p} \text{p}_\text{p}}}\!\) \(a(41) ~=~ 5\) |
\(\text{p} \text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(a(42) ~=~ 6\) |
\(\text{p}_{\text{p} \text{p}_{\text{p}^\text{p}}}\!\) \(a(43) ~=~ 5\) |
\(\text{p}^\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(44) ~=~ 6\) |
\(\text{p}_\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(45) ~=~ 6\) |
|
\(\text{p} \text{p}_{\text{p}_\text{p}^\text{p}}\!\) \(a(46) ~=~ 5\) |
\(\text{p}_{\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(a(47) ~=~ 6\) |
\(\text{p}^{\text{p}^\text{p}} \text{p}_\text{p}\!\) \(a(48) ~=~ 5\) |
\(\text{p}_{\text{p}^\text{p}}^\text{p}\!\) \(a(49) ~=~ 4\) |
\(\text{p} \text{p}_{\text{p}_\text{p}}^\text{p}\!\) \(a(50) ~=~ 5\) |
|
\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(a(51) ~=~ 6\) |
\(\text{p}^\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(a(52) ~=~ 6\) |
\(\text{p}_{\text{p}^{\text{p}^\text{p}}}\!\) \(a(53) ~=~ 4\) |
\(\text{p} \text{p}_\text{p}^{\text{p}_\text{p}}\!\) \(a(54) ~=~ 5\) |
\(\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(55) ~=~ 7\) |
|
\(\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!\) \(a(56) ~=~ 6\) |
\(\text{p}_\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(a(57) ~=~ 6\) |
\(\text{p} \text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(a(58) ~=~ 6\) |
\(\text{p}_{\text{p}_{\text{p}_{\text{p}^\text{p}}}}\!\) \(a(59) ~=~ 5\) |
\(\text{p}^\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(60) ~=~ 7\) |
A062860
- Smallest j with n nodes in its riff (rooted index-functional forest).
|
\(1\!\) \(a(0) ~=~ 1\) |
\(\text{p}\!\) \(a(1) ~=~ 2\) |
\(\text{p}_\text{p}\!\) \(a(2) ~=~ 3\) |
\(\text{p}_{\text{p}_{\text{p}}}\!\) \(a(3) ~=~ 5\) |
\(\text{p} \text{p}_{\text{p}_{\text{p}}}\!\) \(a(4) ~=~ 10\) |
|
\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}}}\!\) \(a(5) ~=~ 15\) |
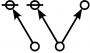
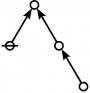
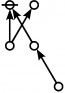
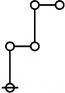
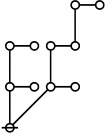
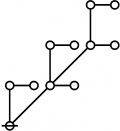
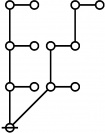
\(\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(6) ~=~ 30\) |
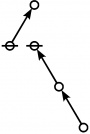
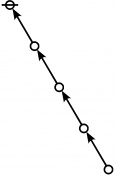
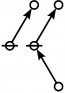
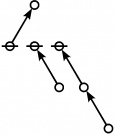
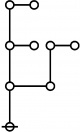
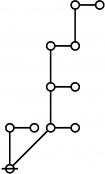
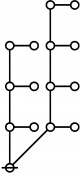
\(\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(7) ~=~ 55\) |
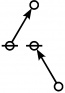
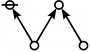
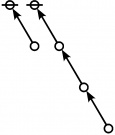
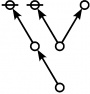
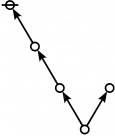
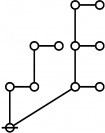
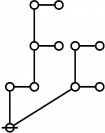
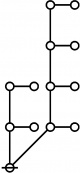
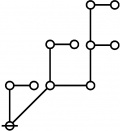
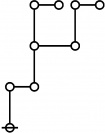
\(\text{p}_\text{p} \text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!\) \(a(8) ~=~ 105\) |
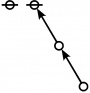
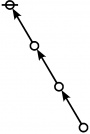
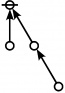
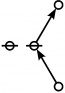
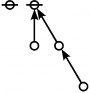
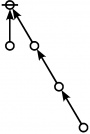
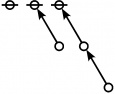
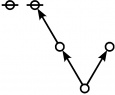
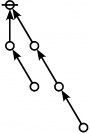
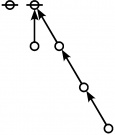
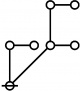
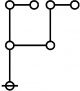
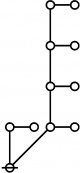
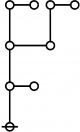
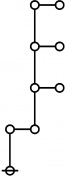
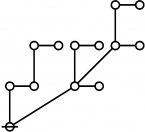
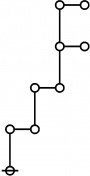
\(\text{p}_\text{p} \text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(9) ~=~ 165\) |
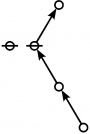
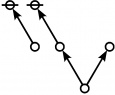
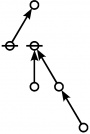
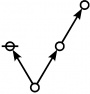
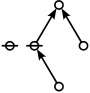
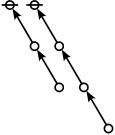
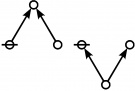
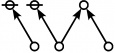
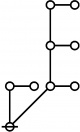
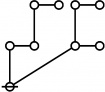
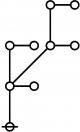
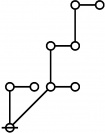
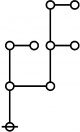
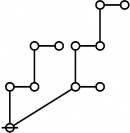
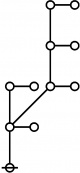
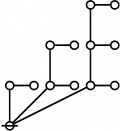
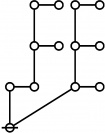
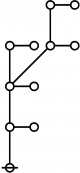
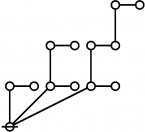
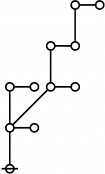
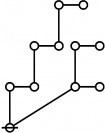
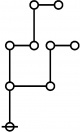
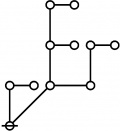
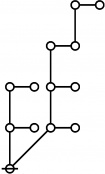
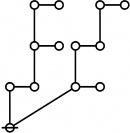
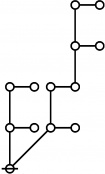
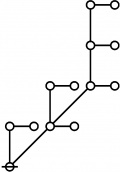
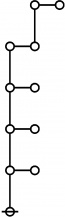
A109301
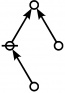
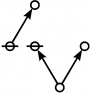
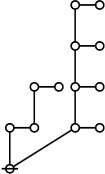
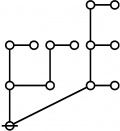
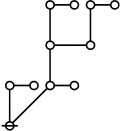
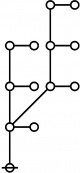
- a(n) = rhig(n) = rote height in gammas of n, where the "rote" corresponding to a positive integer n is a graph derived from the primes factorization of n, as illustrated in the comments.
|
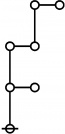
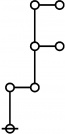
\(1\!\) \(a(1) ~=~ 0\) |
\(\text{p}\!\) \(a(2) ~=~ 1\) |
\(\text{p}_\text{p}\!\) \(a(3) ~=~ 2\) |
\(\text{p}^\text{p}\!\) \(a(4) ~=~ 2\) |
\(\text{p}_{\text{p}_\text{p}}\!\) \(a(5) ~=~ 3\) |
|
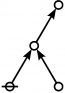
\(\text{p} \text{p}_\text{p}\!\) \(a(6) ~=~ 2\) |
\(\text{p}_{\text{p}^\text{p}}\!\) \(a(7) ~=~ 3\) |
\(\text{p}^{\text{p}_\text{p}}\!\) \(a(8) ~=~ 3\) |
\(\text{p}_\text{p}^\text{p}\!\) \(a(9) ~=~ 2\) |
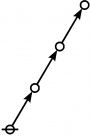
\(\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(10) ~=~ 3\) |
|
\(\text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(11) ~=~ 4\) |
\(\text{p}^\text{p} \text{p}_\text{p}\!\) \(a(12) ~=~ 2\) |
\(\text{p}_{\text{p} \text{p}_\text{p}}\!\) \(a(13) ~=~ 3\) |
\(\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(a(14) ~=~ 3\) |
\(\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(15) ~=~ 3\) |
|
\(\text{p}^{\text{p}^\text{p}}\!\) \(a(16) ~=~ 3\) |
\(\text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(a(17) ~=~ 4\) |
\(\text{p} \text{p}_\text{p}^\text{p}\!\) \(a(18) ~=~ 2\) |
\(\text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(a(19) ~=~ 4\) |
\(\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(20) ~=~ 3\) |
|
\(\text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(a(21) ~=~ 3\) |
\(\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(22) ~=~ 4\) |
\(\text{p}_{\text{p}_\text{p}^\text{p}}\!\) \(a(23) ~=~ 3\) |
\(\text{p}^{\text{p}_\text{p}} \text{p}_\text{p}\!\) \(a(24) ~=~ 3\) |
\(\text{p}_{\text{p}_\text{p}}^\text{p}\!\) \(a(25) ~=~ 3\) |
|
\(\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(a(26) ~=~ 3\) |
\(\text{p}_\text{p}^{\text{p}_\text{p}}\!\) \(a(27) ~=~ 3\) |
\(\text{p}^\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(a(28) ~=~ 3\) |
\(\text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(a(29) ~=~ 4\) |
\(\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(30) ~=~ 3\) |
|
\(\text{p}_{\text{p}_{\text{p}_{\text{p}_\text{p}}}}\!\) \(a(31) ~=~ 5\) |
\(\text{p}^{\text{p}_{\text{p}_\text{p}}}\!\) \(a(32) ~=~ 4\) |
\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(33) ~=~ 4\) |
\(\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(a(34) ~=~ 4\) |
\(\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!\) \(a(35) ~=~ 3\) |
|
\(\text{p}^\text{p} \text{p}_\text{p}^\text{p}\!\) \(a(36) ~=~ 2\) |
\(\text{p}_{\text{p}^\text{p} \text{p}_\text{p}}\!\) \(a(37) ~=~ 3\) |
\(\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(a(38) ~=~ 4\) |
\(\text{p}_\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(a(39) ~=~ 3\) |
\(\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}_\text{p}}\!\) \(a(40) ~=~ 3\) |
|
\(\text{p}_{\text{p}_{\text{p} \text{p}_\text{p}}}\!\) \(a(41) ~=~ 4\) |
\(\text{p} \text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(a(42) ~=~ 3\) |
\(\text{p}_{\text{p} \text{p}_{\text{p}^\text{p}}}\!\) \(a(43) ~=~ 4\) |
\(\text{p}^\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(44) ~=~ 4\) |
\(\text{p}_\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(45) ~=~ 3\) |
|
\(\text{p} \text{p}_{\text{p}_\text{p}^\text{p}}\!\) \(a(46) ~=~ 3\) |
\(\text{p}_{\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(a(47) ~=~ 4\) |
\(\text{p}^{\text{p}^\text{p}} \text{p}_\text{p}\!\) \(a(48) ~=~ 3\) |
\(\text{p}_{\text{p}^\text{p}}^\text{p}\!\) \(a(49) ~=~ 3\) |
\(\text{p} \text{p}_{\text{p}_\text{p}}^\text{p}\!\) \(a(50) ~=~ 3\) |
|
\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(a(51) ~=~ 4\) |
\(\text{p}^\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(a(52) ~=~ 3\) |
\(\text{p}_{\text{p}^{\text{p}^\text{p}}}\!\) \(a(53) ~=~ 4\) |
\(\text{p} \text{p}_\text{p}^{\text{p}_\text{p}}\!\) \(a(54) ~=~ 3\) |
\(\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(55) ~=~ 4\) |
|
\(\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!\) \(a(56) ~=~ 3\) |
\(\text{p}_\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(a(57) ~=~ 4\) |
\(\text{p} \text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(a(58) ~=~ 4\) |
\(\text{p}_{\text{p}_{\text{p}_{\text{p}^\text{p}}}}\!\) \(a(59) ~=~ 5\) |
\(\text{p}^\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(60) ~=~ 3\) |