Difference between revisions of "User:Jon Awbrey/MNO"
Jon Awbrey (talk | contribs) |
Jon Awbrey (talk | contribs) |
||
| Line 3: | Line 3: | ||
==Truth Tables== | ==Truth Tables== | ||
| − | === | + | ===Version 3?=== |
<br> | <br> | ||
| Line 179: | Line 179: | ||
<br> | <br> | ||
| − | === | + | ===Version 2=== |
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="text-align:center; width:90%" | ||
| + | |+ <math>\text{Table 1.}~~\text{Logical Boundaries and Their Complements}</math> | ||
| + | |- style="background:#f0f0ff" | ||
| + | | <math>\mathcal{L}_1</math> | ||
| + | | <math>\mathcal{L}_2</math> | ||
| + | | <math>\mathcal{L}_3</math> | ||
| + | | <math>\mathcal{L}_4</math> | ||
| + | |- style="background:#f0f0ff" | ||
| + | | | ||
| + | | align="right" | <math>p\colon\!</math> | ||
| + | | <math>1~1~1~1~0~0~0~0</math> | ||
| + | | | ||
| + | |- style="background:#f0f0ff" | ||
| + | | | ||
| + | | align="right" | <math>q\colon\!</math> | ||
| + | | <math>1~1~0~0~1~1~0~0</math> | ||
| + | | | ||
| + | |- style="background:#f0f0ff" | ||
| + | | | ||
| + | | align="right" | <math>r\colon\!</math> | ||
| + | | <math>1~0~1~0~1~0~1~0</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_{104} | ||
| + | \\[4pt] | ||
| + | f_{148} | ||
| + | \\[4pt] | ||
| + | f_{146} | ||
| + | \\[4pt] | ||
| + | f_{97} | ||
| + | \\[4pt] | ||
| + | f_{134} | ||
| + | \\[4pt] | ||
| + | f_{73} | ||
| + | \\[4pt] | ||
| + | f_{41} | ||
| + | \\[4pt] | ||
| + | f_{22} | ||
| + | \end{matrix}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_{01101000} | ||
| + | \\[4pt] | ||
| + | f_{10010100} | ||
| + | \\[4pt] | ||
| + | f_{10010010} | ||
| + | \\[4pt] | ||
| + | f_{01100001} | ||
| + | \\[4pt] | ||
| + | f_{10000110} | ||
| + | \\[4pt] | ||
| + | f_{01001001} | ||
| + | \\[4pt] | ||
| + | f_{00101001} | ||
| + | \\[4pt] | ||
| + | f_{00010110} | ||
| + | \end{matrix}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | 0~1~1~0~1~0~0~0 | ||
| + | \\[4pt] | ||
| + | 1~0~0~1~0~1~0~0 | ||
| + | \\[4pt] | ||
| + | 1~0~0~1~0~0~1~0 | ||
| + | \\[4pt] | ||
| + | 0~1~1~0~0~0~0~1 | ||
| + | \\[4pt] | ||
| + | 1~0~0~0~0~1~1~0 | ||
| + | \\[4pt] | ||
| + | 0~1~0~0~1~0~0~1 | ||
| + | \\[4pt] | ||
| + | 0~0~1~0~1~0~0~1 | ||
| + | \\[4pt] | ||
| + | 0~0~0~1~0~1~1~0 | ||
| + | \end{matrix}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ( p , q , r ) | ||
| + | \\[4pt] | ||
| + | ( p , q , (r)) | ||
| + | \\[4pt] | ||
| + | ( p , (q), r ) | ||
| + | \\[4pt] | ||
| + | ( p , (q), (r)) | ||
| + | \\[4pt] | ||
| + | ((p), q , r ) | ||
| + | \\[4pt] | ||
| + | ((p), q , (r)) | ||
| + | \\[4pt] | ||
| + | ((p), (q), r ) | ||
| + | \\[4pt] | ||
| + | ((p), (q), (r)) | ||
| + | \end{matrix}</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_{233} | ||
| + | \\[4pt] | ||
| + | f_{214} | ||
| + | \\[4pt] | ||
| + | f_{182} | ||
| + | \\[4pt] | ||
| + | f_{121} | ||
| + | \\[4pt] | ||
| + | f_{158} | ||
| + | \\[4pt] | ||
| + | f_{109} | ||
| + | \\[4pt] | ||
| + | f_{107} | ||
| + | \\[4pt] | ||
| + | f_{151} | ||
| + | \end{matrix}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_{11101001} | ||
| + | \\[4pt] | ||
| + | f_{11010110} | ||
| + | \\[4pt] | ||
| + | f_{10110110} | ||
| + | \\[4pt] | ||
| + | f_{01111001} | ||
| + | \\[4pt] | ||
| + | f_{10011110} | ||
| + | \\[4pt] | ||
| + | f_{01101101} | ||
| + | \\[4pt] | ||
| + | f_{01101011} | ||
| + | \\[4pt] | ||
| + | f_{10010111} | ||
| + | \end{matrix}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | 1~1~1~0~1~0~0~1 | ||
| + | \\[4pt] | ||
| + | 1~1~0~1~0~1~1~0 | ||
| + | \\[4pt] | ||
| + | 1~0~1~1~0~1~1~0 | ||
| + | \\[4pt] | ||
| + | 0~1~1~1~1~0~0~1 | ||
| + | \\[4pt] | ||
| + | 1~0~0~1~1~1~1~0 | ||
| + | \\[4pt] | ||
| + | 0~1~1~0~1~1~0~1 | ||
| + | \\[4pt] | ||
| + | 0~1~1~0~1~0~1~1 | ||
| + | \\[4pt] | ||
| + | 1~0~0~1~0~1~1~1 | ||
| + | \end{matrix}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (((p), (q), (r))) | ||
| + | \\[4pt] | ||
| + | (((p), (q), r )) | ||
| + | \\[4pt] | ||
| + | (((p), q , (r))) | ||
| + | \\[4pt] | ||
| + | (((p), q , r )) | ||
| + | \\[4pt] | ||
| + | (( p , (q), (r))) | ||
| + | \\[4pt] | ||
| + | (( p , (q), r )) | ||
| + | \\[4pt] | ||
| + | (( p , q , (r))) | ||
| + | \\[4pt] | ||
| + | (( p , q , r )) | ||
| + | \end{matrix}</math> | ||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | ===Version 1=== | ||
<br> | <br> | ||
Revision as of 16:16, 23 August 2009
Logical Graphs
Truth Tables
Version 3?
| \(\mathcal{L}_1\) | \(\mathcal{L}_2\) | \(\mathcal{L}_3\) | \(\mathcal{L}_4\) |
| \(p\colon\!\) | \(1~1~1~1~0~0~0~0\) | ||
| \(q\colon\!\) | \(1~1~0~0~1~1~0~0\) | ||
| \(r\colon\!\) | \(1~0~1~0~1~0~1~0\) | ||
|
\(\begin{matrix} f_{104} \\[4pt] f_{148} \\[4pt] f_{146} \\[4pt] f_{97} \\[4pt] f_{134} \\[4pt] f_{73} \\[4pt] f_{41} \\[4pt] f_{22} \end{matrix}\) |
\(\begin{matrix} f_{01101000} \\[4pt] f_{10010100} \\[4pt] f_{10010010} \\[4pt] f_{01100001} \\[4pt] f_{10000110} \\[4pt] f_{01001001} \\[4pt] f_{00101001} \\[4pt] f_{00010110} \end{matrix}\) |
\(\begin{matrix} 0~1~1~0~1~0~0~0 \\[4pt] 1~0~0~1~0~1~0~0 \\[4pt] 1~0~0~1~0~0~1~0 \\[4pt] 0~1~1~0~0~0~0~1 \\[4pt] 1~0~0~0~0~1~1~0 \\[4pt] 0~1~0~0~1~0~0~1 \\[4pt] 0~0~1~0~1~0~0~1 \\[4pt] 0~0~0~1~0~1~1~0 \end{matrix}\) |
\(\begin{matrix} ( p , q , r ) \\[4pt] ( p , q , (r)) \\[4pt] ( p , (q), r ) \\[4pt] ( p , (q), (r)) \\[4pt] ((p), q , r ) \\[4pt] ((p), q , (r)) \\[4pt] ((p), (q), r ) \\[4pt] ((p), (q), (r)) \end{matrix}\) |
|
\(\begin{matrix} f_{233} \\[4pt] f_{214} \\[4pt] f_{182} \\[4pt] f_{121} \\[4pt] f_{158} \\[4pt] f_{109} \\[4pt] f_{107} \\[4pt] f_{151} \end{matrix}\) |
\(\begin{matrix} f_{11101001} \\[4pt] f_{11010110} \\[4pt] f_{10110110} \\[4pt] f_{01111001} \\[4pt] f_{10011110} \\[4pt] f_{01101101} \\[4pt] f_{01101011} \\[4pt] f_{10010111} \end{matrix}\) |
\(\begin{matrix} 1~1~1~0~1~0~0~1 \\[4pt] 1~1~0~1~0~1~1~0 \\[4pt] 1~0~1~1~0~1~1~0 \\[4pt] 0~1~1~1~1~0~0~1 \\[4pt] 1~0~0~1~1~1~1~0 \\[4pt] 0~1~1~0~1~1~0~1 \\[4pt] 0~1~1~0~1~0~1~1 \\[4pt] 1~0~0~1~0~1~1~1 \end{matrix}\) |
\(\begin{matrix} (((p), (q), (r))) \\[4pt] (((p), (q), r )) \\[4pt] (((p), q , (r))) \\[4pt] (((p), q , r )) \\[4pt] (( p , (q), (r))) \\[4pt] (( p , (q), r )) \\[4pt] (( p , q , (r))) \\[4pt] (( p , q , r )) \end{matrix}\) |
Version 2
| \(\mathcal{L}_1\) | \(\mathcal{L}_2\) | \(\mathcal{L}_3\) | \(\mathcal{L}_4\) |
| \(p\colon\!\) | \(1~1~1~1~0~0~0~0\) | ||
| \(q\colon\!\) | \(1~1~0~0~1~1~0~0\) | ||
| \(r\colon\!\) | \(1~0~1~0~1~0~1~0\) | ||
|
\(\begin{matrix} f_{104} \\[4pt] f_{148} \\[4pt] f_{146} \\[4pt] f_{97} \\[4pt] f_{134} \\[4pt] f_{73} \\[4pt] f_{41} \\[4pt] f_{22} \end{matrix}\) |
\(\begin{matrix} f_{01101000} \\[4pt] f_{10010100} \\[4pt] f_{10010010} \\[4pt] f_{01100001} \\[4pt] f_{10000110} \\[4pt] f_{01001001} \\[4pt] f_{00101001} \\[4pt] f_{00010110} \end{matrix}\) |
\(\begin{matrix} 0~1~1~0~1~0~0~0 \\[4pt] 1~0~0~1~0~1~0~0 \\[4pt] 1~0~0~1~0~0~1~0 \\[4pt] 0~1~1~0~0~0~0~1 \\[4pt] 1~0~0~0~0~1~1~0 \\[4pt] 0~1~0~0~1~0~0~1 \\[4pt] 0~0~1~0~1~0~0~1 \\[4pt] 0~0~0~1~0~1~1~0 \end{matrix}\) |
\(\begin{matrix} ( p , q , r ) \\[4pt] ( p , q , (r)) \\[4pt] ( p , (q), r ) \\[4pt] ( p , (q), (r)) \\[4pt] ((p), q , r ) \\[4pt] ((p), q , (r)) \\[4pt] ((p), (q), r ) \\[4pt] ((p), (q), (r)) \end{matrix}\) |
|
\(\begin{matrix} f_{233} \\[4pt] f_{214} \\[4pt] f_{182} \\[4pt] f_{121} \\[4pt] f_{158} \\[4pt] f_{109} \\[4pt] f_{107} \\[4pt] f_{151} \end{matrix}\) |
\(\begin{matrix} f_{11101001} \\[4pt] f_{11010110} \\[4pt] f_{10110110} \\[4pt] f_{01111001} \\[4pt] f_{10011110} \\[4pt] f_{01101101} \\[4pt] f_{01101011} \\[4pt] f_{10010111} \end{matrix}\) |
\(\begin{matrix} 1~1~1~0~1~0~0~1 \\[4pt] 1~1~0~1~0~1~1~0 \\[4pt] 1~0~1~1~0~1~1~0 \\[4pt] 0~1~1~1~1~0~0~1 \\[4pt] 1~0~0~1~1~1~1~0 \\[4pt] 0~1~1~0~1~1~0~1 \\[4pt] 0~1~1~0~1~0~1~1 \\[4pt] 1~0~0~1~0~1~1~1 \end{matrix}\) |
\(\begin{matrix} (((p), (q), (r))) \\[4pt] (((p), (q), r )) \\[4pt] (((p), q , (r))) \\[4pt] (((p), q , r )) \\[4pt] (( p , (q), (r))) \\[4pt] (( p , (q), r )) \\[4pt] (( p , q , (r))) \\[4pt] (( p , q , r )) \end{matrix}\) |
Version 1
| \(\mathcal{L}_1\) | \(\mathcal{L}_2\) | \(\mathcal{L}_3\) | \(\mathcal{L}_4\) |
| \(p =\!\) | 1 1 1 1 0 0 0 0 | ||
| \(q =\!\) | 1 1 0 0 1 1 0 0 | ||
| \(r =\!\) | 1 0 1 0 1 0 1 0 |
| \(f_{104}\!\) | \(f_{01101000}\!\) | 0 1 1 0 1 0 0 0 | \(( p , q , r )\!\) |
| \(f_{148}\!\) | \(f_{10010100}\!\) | 1 0 0 1 0 1 0 0 | \(( p , q , (r))\!\) |
| \(f_{146}\!\) | \(f_{10010010}\!\) | 1 0 0 1 0 0 1 0 | \(( p , (q), r )\!\) |
| \(f_{97}\!\) | \(f_{01100001}\!\) | 0 1 1 0 0 0 0 1 | \(( p , (q), (r))\!\) |
| \(f_{134}\!\) | \(f_{10000110}\!\) | 1 0 0 0 0 1 1 0 | \(((p), q , r )\!\) |
| \(f_{73}\!\) | \(f_{01001001}\!\) | 0 1 0 0 1 0 0 1 | \(((p), q , (r))\!\) |
| \(f_{41}\!\) | \(f_{00101001}\!\) | 0 0 1 0 1 0 0 1 | \(((p), (q), r )\!\) |
| \(f_{22}\!\) | \(f_{00010110}\!\) | 0 0 0 1 0 1 1 0 | \(((p), (q), (r))\!\) |
| \(f_{233}\!\) | \(f_{11101001}\!\) | 1 1 1 0 1 0 0 1 | \((((p), (q), (r)))\!\) |
| \(f_{214}\!\) | \(f_{11010110}\!\) | 1 1 0 1 0 1 1 0 | \((((p), (q), r ))\!\) |
| \(f_{182}\!\) | \(f_{10110110}\!\) | 1 0 1 1 0 1 1 0 | \((((p), q , (r)))\!\) |
| \(f_{121}\!\) | \(f_{01111001}\!\) | 0 1 1 1 1 0 0 1 | \((((p), q , r ))\!\) |
| \(f_{158}\!\) | \(f_{10011110}\!\) | 1 0 0 1 1 1 1 0 | \((( p , (q), (r)))\!\) |
| \(f_{109}\!\) | \(f_{01101101}\!\) | 0 1 1 0 1 1 0 1 | \((( p , (q), r ))\!\) |
| \(f_{107}\!\) | \(f_{01101011}\!\) | 0 1 1 0 1 0 1 1 | \((( p , q , (r)))\!\) |
| \(f_{151}\!\) | \(f_{10010111}\!\) | 1 0 0 1 0 1 1 1 | \((( p , q , r ))\!\) |
Venn Diagrams
New Version
|
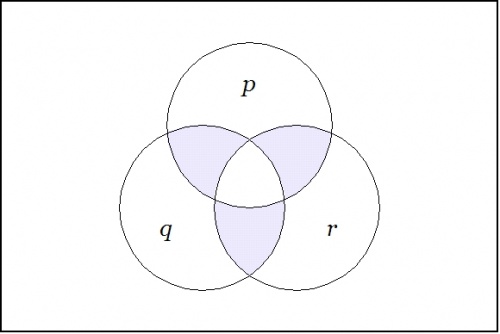
\(\text{Figure 2.} ~~ \texttt{(} p \texttt{,} q \texttt{,} r \texttt{)}\) |
|
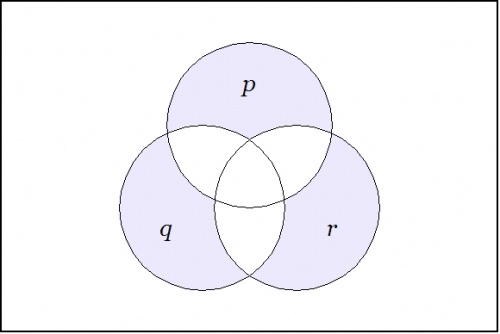
\(\text{Figure 3.} ~~ \texttt{((} p \texttt{),(} q \texttt{),(} r \texttt{))}\) |
Old Version
|
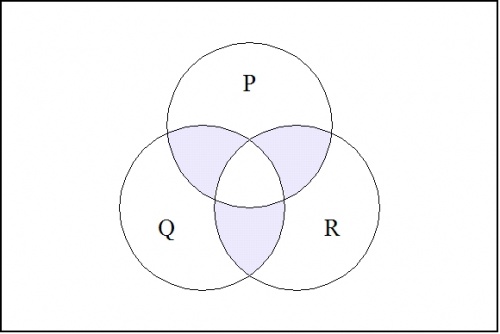
\(\text{Figure 2.} ~~ \texttt{(} p \texttt{,} q \texttt{,} r \texttt{)}\) |
|
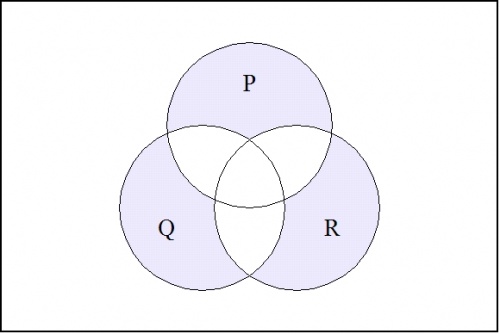
\(\text{Figure 3.} ~~ \texttt{((} p \texttt{),(} q \texttt{),(} r \texttt{))}\) |